Coordinate measuring machine accuracy on the shop floor
Coordinate measuring machine (CMM) accuracy is dependent upon the ambient thermal environment in which it operates.
Contact us
Coordinate measuring machine (CMM) accuracy is dependent upon the ambient thermal environment in which it operates. Changes in temperature cause the scales, machine structure and artifacts being measured to expand, contract, and, in some cases, distort in a non-linear manner.
Though often compensated for in a variety of ways, these thermally induced changes can lead to significant measurement uncertainty, particularly in the context of measurement on the shop floor, where temperature can be difficult to control. With the ever-continuing trend of moving dimensional inspection from thermally controlled metrology labs to the shop floor, understanding how temperature affects CMM accuracy is more important than ever before.
Traditionally, the thermal dependence of a CMM’s accuracy has been specified using broad temperature bands centered about 20°C (68°F). For instance, a manufacturer might specify a hypothetical CMM’s maximum permissible error of indication for size measurement, MPEE, according to ISO 10360-2 over a temperature band of 18-22°C (64-72°F) as:
MPEE = 3.0 + 3.0 * L / 1000
Where MPEE is in microns, and L is the measurement length in millimeters.
While this is a logical way (for both the CMM manufacturer and the customer) to specify the temperature dependence of CMM accuracy for a machine in a lab environment, the logic falls apart for machines installed and used in an environment where the temperature is not well controlled over both long and short time scales.
While a single temperature band specification (whether it is wide or narrow) is convenient for the CMM manufacturer, the customer is left with only the manufacturer’s conservative, but not terribly detailed estimate of how machine accuracy changes with temperature. After all, a primary reason customers purchase a shop-floor machine is to position it in a location where the ambient temperature will, in all likelihood, affect the CMM’s measurement accuracy.
Though often compensated for in a variety of ways, these thermally induced changes can lead to significant measurement uncertainty, particularly in the context of measurement on the shop floor, where temperature can be difficult to control. With the ever-continuing trend of moving dimensional inspection from thermally controlled metrology labs to the shop floor, understanding how temperature affects CMM accuracy is more important than ever before.
Traditionally, the thermal dependence of a CMM’s accuracy has been specified using broad temperature bands centered about 20°C (68°F). For instance, a manufacturer might specify a hypothetical CMM’s maximum permissible error of indication for size measurement, MPEE, according to ISO 10360-2 over a temperature band of 18-22°C (64-72°F) as:
MPEE = 3.0 + 3.0 * L / 1000
Where MPEE is in microns, and L is the measurement length in millimeters.
While this is a logical way (for both the CMM manufacturer and the customer) to specify the temperature dependence of CMM accuracy for a machine in a lab environment, the logic falls apart for machines installed and used in an environment where the temperature is not well controlled over both long and short time scales.
While a single temperature band specification (whether it is wide or narrow) is convenient for the CMM manufacturer, the customer is left with only the manufacturer’s conservative, but not terribly detailed estimate of how machine accuracy changes with temperature. After all, a primary reason customers purchase a shop-floor machine is to position it in a location where the ambient temperature will, in all likelihood, affect the CMM’s measurement accuracy.
Stair-step specifications
Typically, CMM manufacturers have attempted to deal with this problem by specifying accuracy by way of multiple temperature bands. Again, consider a hypothetical CMM with accuracy specified as:
MPEE = 3.0 + 3.0 * L / 1000 (18-22°C)
MPEE = 3.3 + 4.2 * L / 1000 (16-26°C)
MPEE = 3.5 + 5.0 * L / 1000 (15-30°C)
With a measuring length L of 500 mm, this is portrayed graphically as a step function of ambient temperature.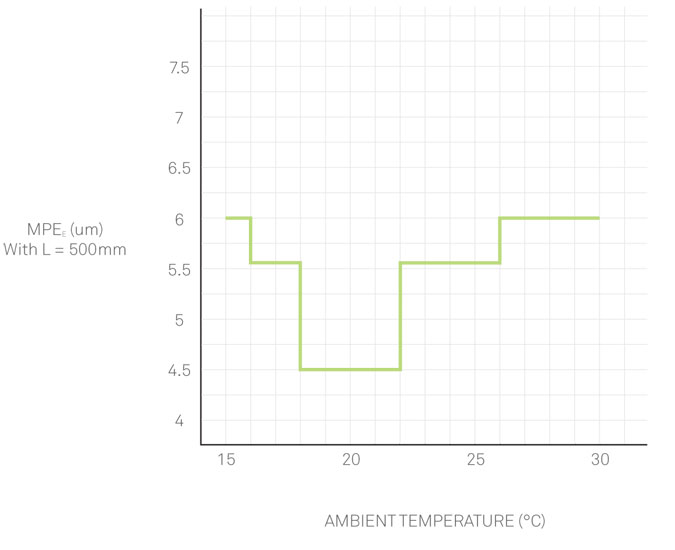
MPEE = 3.0 + 3.0 * L / 1000 (18-22°C)
MPEE = 3.3 + 4.2 * L / 1000 (16-26°C)
MPEE = 3.5 + 5.0 * L / 1000 (15-30°C)
With a measuring length L of 500 mm, this is portrayed graphically as a step function of ambient temperature.

Continuous thermal specifications
Considering the physics involved when metrology frames expand, contract and distort with changes in temperature, we intuitively know that this type of step function is inaccurate. Metrology structures do not normally exhibit changes in accuracy as a step function of temperature, with instantaneous degradations in accuracy occurring when the temperature crosses some threshold value. Or, if they did exist, we probably would not want to make measurements with them.
Clearly, a more detailed description of CMM accuracy under varying ambient temperature conditions is needed in environments that lack sufficient thermal controls. A more physically realistic alternative is the specification of accuracy as a continuous function of ambient temperature. And from the pragmatic viewpoint of the metrologist or quality engineer, it is eminently more useful.
To illustrate the point, let’s take a look at an actual CMM. Consider the accuracy statement of the 4.5.4 SF shop floor CMM:
MPEE = 3.1 + 0.05 * ∆T + (3.0 + 0.2 * ∆T) * L / 1000 (15-40°C)
Where ∆T is the departure of ambient temperature from 20°C.
Again, let’s consider a measuring length of 500 mm and plot MPEE as a function of ambient temperature. This time we find a more physically intuitive result and one that is much more useful to the metrology practitioner.
The usefulness is further demonstrated when we display on the same graph the previous hypothetical example where performance was specified over a series of broad thermal ranges.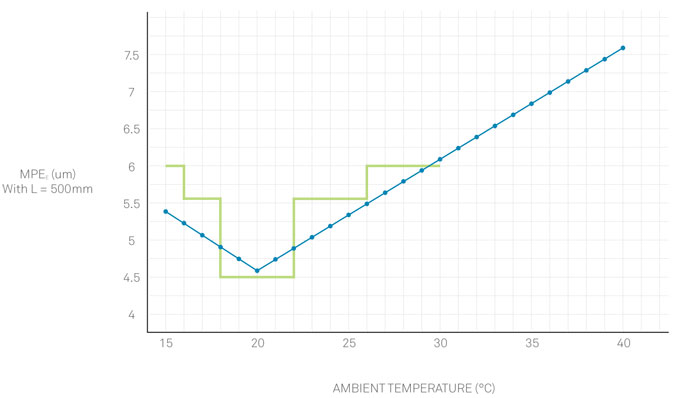
In addition to providing the user with a more precise picture of the CMM’s accuracy at varying temperatures, a continuous specification is a compact and elegant way of defining machine accuracy specifications and is particularly well suited to being incorporated into automated reporting of measurement results.
Clearly, a more detailed description of CMM accuracy under varying ambient temperature conditions is needed in environments that lack sufficient thermal controls. A more physically realistic alternative is the specification of accuracy as a continuous function of ambient temperature. And from the pragmatic viewpoint of the metrologist or quality engineer, it is eminently more useful.
To illustrate the point, let’s take a look at an actual CMM. Consider the accuracy statement of the 4.5.4 SF shop floor CMM:
MPEE = 3.1 + 0.05 * ∆T + (3.0 + 0.2 * ∆T) * L / 1000 (15-40°C)
Where ∆T is the departure of ambient temperature from 20°C.
Again, let’s consider a measuring length of 500 mm and plot MPEE as a function of ambient temperature. This time we find a more physically intuitive result and one that is much more useful to the metrology practitioner.
The usefulness is further demonstrated when we display on the same graph the previous hypothetical example where performance was specified over a series of broad thermal ranges.

In addition to providing the user with a more precise picture of the CMM’s accuracy at varying temperatures, a continuous specification is a compact and elegant way of defining machine accuracy specifications and is particularly well suited to being incorporated into automated reporting of measurement results.
Temperature variation over time
Another factor to take into consideration when one is equipped with an extended temperature range specification, continuous or not, is the permissible temperature changes that the manufacturer specifies over time. Normally this is expressed as the change within a 1-hour and a 24-hour period. This specification tells the user how much temperature variation is allowed over a given time interval in order to maintain the specified accuracy performance. A larger permitted change in a given period means the machine is better able to cope with changing shop thermal conditions.
Practical advice for shop-floor deployment of a CMM
When choosing to deploy a CMM on the shop floor, it is important to evaluate the measurement tasks to be performed and calculate an uncertainty budget. Then, calculate the accuracy of the machine using a continuous thermal specification at all of the different temperatures that your shop may encounter, making sure that you do not exceed the total thermal variation per hour or per day. This gives you the expected accuracy of the machine at any time of the day. If the machine accuracy is acceptable to your uncertainty budget at all times, great! You can use your machine all day long. If not, then you must consider alternatives, such as only using the machine at certain times of the day, or running parts with looser tolerances during times when the shop is warmest.
The use of a CMM with a continuous thermal specification on the shop floor equips the CMM user with a more complete picture of a machine’s expected performance in an uncontrolled environment. This enables better decision making and more confidence in measurement results. One such CMM is the 4.5.4SF shop floor machine.
The use of a CMM with a continuous thermal specification on the shop floor equips the CMM user with a more complete picture of a machine’s expected performance in an uncontrolled environment. This enables better decision making and more confidence in measurement results. One such CMM is the 4.5.4SF shop floor machine.