Simulazione del dispiegamento di un modulo spaziale tramite meccanismi ad aste flessibili

Negli ultimi anni, la tecnologia inflatable (gonfiabile) sta sempre più prendendo piede nell’ambito dell’esplorazione spaziale. Il loro scopo è quello di, una volta trasportati gli strumenti dalla Terra all’orbita di operatività, permettere a questi di aumentare il loro volume attraverso un processo definito “dispiegamento”.

L’esplorazione spaziale però è strettamente collegata anche alla sopravvivenza degli astronauti in ambiente ostile. Per questo si è proposto di ricreare una serra idroponica inflatable che possa permettere la creazione/smaltimento di ossigeno e anidride carbonica e la coltivazione di specie vegetali in orbita.

La parte più importante di questa tecnologia è il dispositivo che permette il dispiegamento, il “Deployable boom”.

Il termine “Boom dispiegabile" fa riferimento alla famiglia delle strutture ad aste sottili flessibili, cioè una speciale tipologia di strutture che sono in grado di modificare la propria forma e adottare delle configurazioni appositamente progettate (come detto precedentemente passare da una configurazione compatta a dispiegata). Grazie alle loro proprietà di leggerezza e spessore minimo, sono fondamentali in ambiti dove il peso e l’ingombro devono essere minimi.

Per mezzo del programma di calcolo MATLAB, è stato sviluppato un codice che potesse risolvere un modello di ottimizzazione utilizzando il metodo di programmazione quadratica sequenziale. Lo scopo del boom in questione è quello di traslare una massa, corrispondente alla parete della serra, di circa 24 Kg, ovvero il peso della struttura e della parte elettronica.

Quindi, nota questa e assegnati dei vincoli, Matlab processa i dati (diametro del boom, spessore del materiale, raggio del rocchetto) al fine di stabilire la dimensione ottimale del boom. Questa è definita attraverso il parametro “k”, il quale indica di quanto si deve ingrandire la struttura al fine di traslare quella particolare massa.

Imponendo un fattore di sicurezza Ks = 1.5 (al fine di essere certi che il dispositivo possa spostare anche più del valore nominale di progetto in caso di failoure), il boom deve traslare circa 350N.

Il boom generico, quindi, deve essere ingrandito di 2.23 volte per sopperire alla richiesta e se ne possono installare 3: 2 necessari al completamento del dispiegamento ed uno per ridondanza.

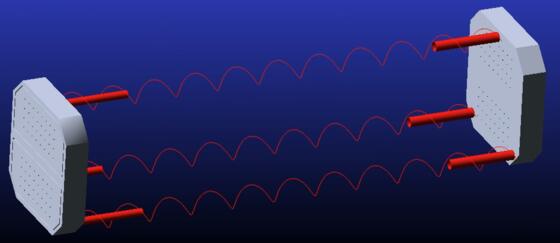
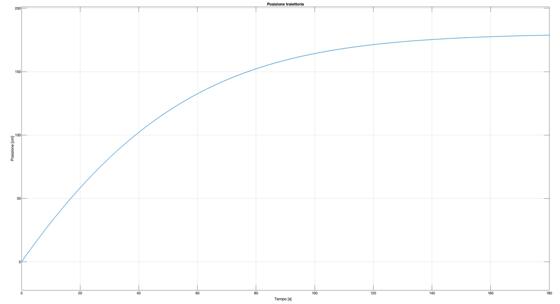
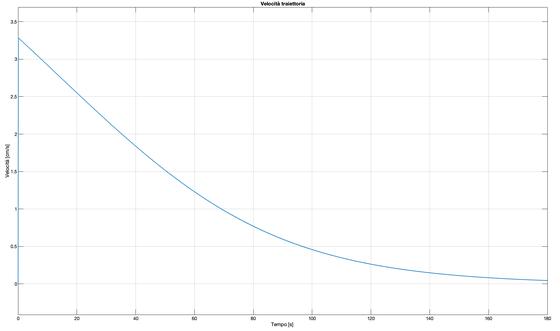
Inizialmente, per semplicità progettuale, in Adams i deployable boom sono stati rappresentati da Spring - Dampers, cioè molle torsionali che permettono di spingere una massa con assegnati precarico e coefficiente di smorzamento, identificando così l’andamento di posizione e velocità rappresentato in figura.

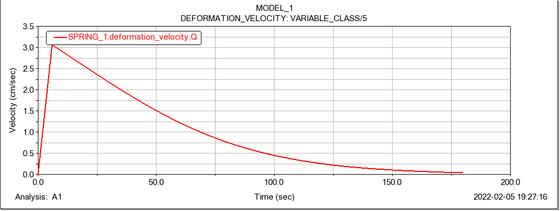
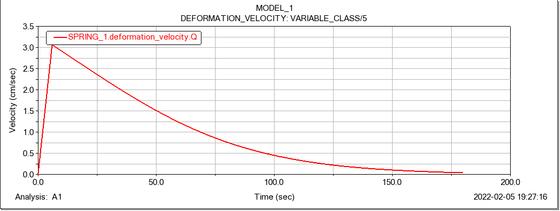
Successivamente, è stato necessario sviluppare un controllore affinché la velocità di dispiegamento del boom fosse controllata e che la lunghezza finale di 180 cm fosse raggiunta in 180 secondi: un dispiegamento lento, infatti, riesce a prevenire problemi di vibrazioni e condizioni incontrollate che possono recare criticità alla struttura. 

È stata così proposta inizialmente un’analisi tramite il software di simulazione Simulink sviluppando e comparando due tipi di controllori, poi se n’è analizzato un terzo.

I controllori sono:

• uno Proporzionale Integrativo Derivativo (PID), che risulta essere il più semplice, il più economico dal punto di vista computazionale ma più suscettibile a condizioni non perfettamente controllate;
• uno Feed-forward feed-back Adattivo, che risulta più complesso sia dal punto di vista costruttivo che di calcolo. Questo crea uno stato predittivo e lo confronta con quello reale, creando un sistema che si adatta alle configurazioni e che permette di avere ottime performance anche in condizioni difficili da controllare;
• uno derivato dalla cosimulazione Adams-Simulink basato sul controllore PID: i punti di dispiegamento vengono calcolati attraverso Adams e Simulink ne controlla l’andamento. 

 La scelta migliore è ricaduta proprio sul terzo caso.

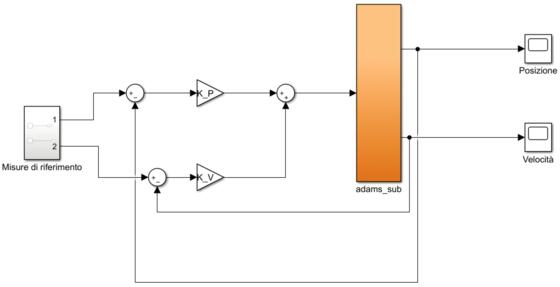
• Costruire il modello Adams delle molle di reazione;
• Creare gli input ed output, cioè le variabili da controllare nella simulazione (in questo caso posizione e velocità);
• Costruire il diagramma a blocchi con Simulink;
• Simulare il modello combinato.

In questo modo Adams e Simulink lavoreranno congiuntamente per il calcolo di posizione e velocità, lavorando con un passo tempo molto fitto (si è scelto 1 millesimo di secondo).

I risultati sono molto simili a quelli calcolati nel solo controllore PID ma la simulazione risulta avere un costo computazionale minore nel caso dell’utilizzo di solo Simulink.

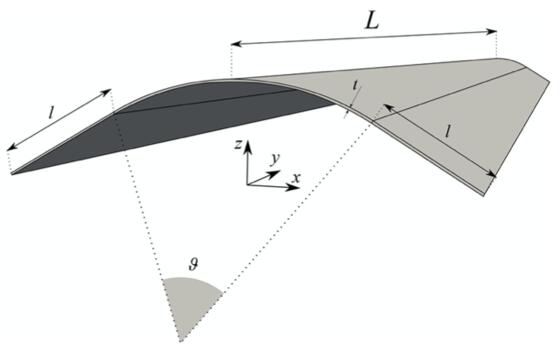
Infine, l’attenzione si è focalizzata sui Tape Spring, definiti come strisce elastiche in parete sottile, caratterizzate da un raggio di curvatura “r” e da un arco di circonferenza con angolo “theta”.

La particolarità sta proprio nel poter essere arrotolati e dispiegati elasticamente. Quando vengono arrotolati immagazzinano energia potenziale elastica che viene rilasciata quando si dispiegano. Non dispongono di elementi meccanici come cerniere, il che le rende particolarmente compatibili in capo spaziale dove la leggerezza e la semplicità sono elementi fondamentali.

È stato analizzato (mediante Fisher Machine) il tipico diagramma Momento - Angolo di deflessione [M – theta] per risultati sperimentali e per CUF (Carrera Unified Formulation), e successivamente è stato comparato con l’analisi su Adams.

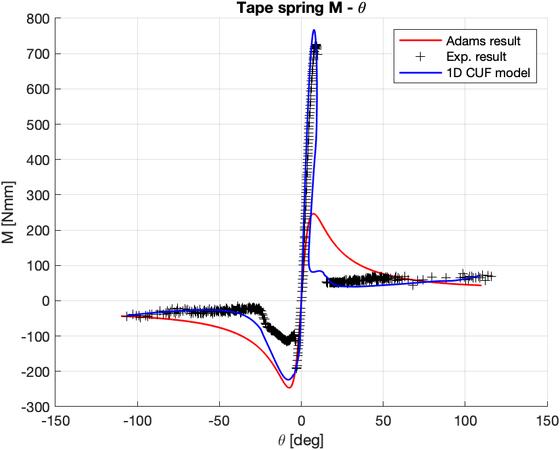
Dal confronto è evidente come i valori siano pressoché identici in campo lineare (durante le prime rotazioni) e si discostano quando, per rotazioni theta sempre più importanti, la deflessione della struttura si fa più pronunciata. Questo è da attribuirsi al fatto che il modello in Adams è stato creato con lo strumento Fe Part che fa riferimento alla formulazione ANCF, tipica delle strutture a guscio. Questa utilizza degli elementi del tutto simili al classico modello trave di Eulero-Bernoulli, i quali presuppongono che la sezione trasversale (e quindi i contorni) rimangano rigidi e perpendicolari alla superficie neutra durante le deformazioni.

Si conclude quindi che sviluppare dispositivi dinamici e complessi su Adams è possibile, con semplicità e con risultati promettenti. Al fine però di superare le limitazioni viste nei diagrammi precedenti, si consiglia l’utilizzo di software che, grazie a formulazioni più complete, riescono ad effettuare un’analisi migliore e più precisa. Si consiglia infatti, per il parziale completamento del progetto, l’utilizzo del software MSC Marc, ottimizzato per l’analisi non-lineare ad elementi finiti.

Autore: Stefano Barletta

Relatori:

Prof. Alfonso PAGANI
Prof. Riccardo AUGELLO
Prof. Erasmo CARRER