Introduction à la mesure de coordonnées
Comprendre le principe de fonctionnement de la MMT: le système de coordonnées.
Contactez-nous
Nous utilisons un système de coordonnées pour décrire les mouvements d’une machine à mesurer. Inventé par le célèbre philosophe et mathématicien René Descartes au début des années 1600, le système de coordonnées nous permet de localiser des éléments par rapport à d'autres éléments sur des pièces.
Un système de coordonnées ressemble à une carte de niveaux où la combinaison d’une lettre sur un bord de la carte, avec un nombre de l’autre côté et des élévations, décrit de façon unique chaque emplacement sur la carte. Cette combinaison de lettre/nombre/élévation est désignée par coordonnée et représente une position spécifique par rapport à toutes les autres.
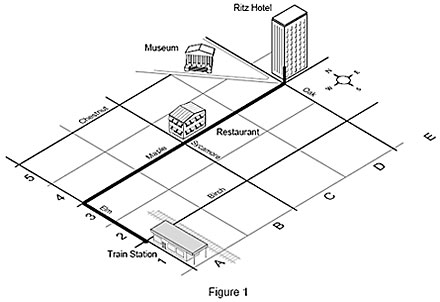
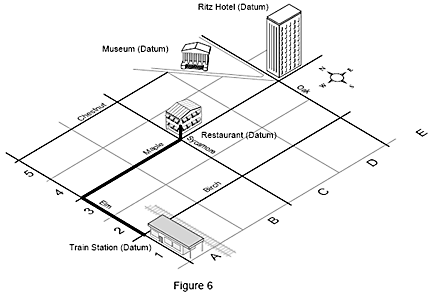
Un autre exemple est un plan de ville montrant des bâtiments. Pour vous rendre à votre chambre dans l’hôtel Ritz à partir de la gare (votre origine), vous parcourez 2 blocs le long d’Elm Street, 4 blocs sur Maple Street et montez 3 étages au Ritz. Il est également possible de décrire cet emplacement avec les coordonnées 4-E-3 sur le plan, ce qui correspondrait aux axes X, Y et Z de la machine. Ces coordonnées décrivent de façon unique votre chambre, et aucun autre emplacement sur le plan.
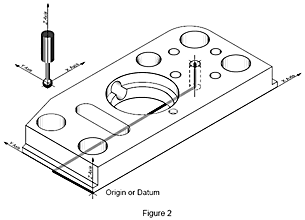
Une machine à mesurer tridimensionnelle (MMT) applique le même principe que votre doigt qui suit les coordonnées d’un plan. Les trois axes forment le système de coordonnées de la machine. Au lieu d'un doigt, la MMT utilise un palpeur pour mesurer des points sur une pièce. Chaque point sur la pièce est unique par rapport au système de coordonnées de la machine. La MMT combine les points mesurés pour former un élément que l’on peut maintenant déterminer par rapport à tous les autres éléments.
Le système de coordonnées : le système de coordonnées de la machine
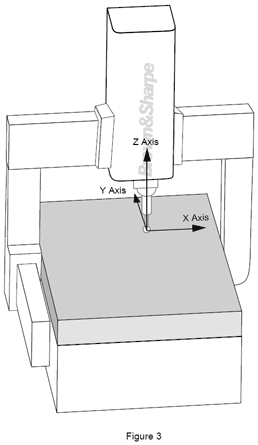
Il y a deux types de systèmes de coordonnées dans l’univers des mesures. Le premier est le système de coordonnées de la machine Les axes X, Y et Z se réfèrent aux mouvements de la machine. Vu de la face avant de la machine, l’axe X va de gauche à droite, l’axe Y de l’avant vers l'arrière et l’axe Z de haut en bas, perpendiculairement aux deux autres.
Le système de coordonnées : le système de coordonnées de la pièce
Le deuxième système de coordonnées est le système de coordonnées de la pièce, où les trois axes se rapportent aux référentiels ou caractéristiques de la pièce.
Avant l’introduction du logiciel informatique pour la mesure de coordonnées, on positionnait physiquement les pièces parallèlement aux axes de la machine de façon que les systèmes de coordonnées de la machine et de la pièce soient parallèles. C’était une opération très laborieuse et assez imprécise. Lorsque la pièce était ronde ou profilée plutôt que carrée ou rectangulaire, la tâche de mesure devenait pratiquement impossible.
Avant l’introduction du logiciel informatique pour la mesure de coordonnées, on positionnait physiquement les pièces parallèlement aux axes de la machine de façon que les systèmes de coordonnées de la machine et de la pièce soient parallèles. C’était une opération très laborieuse et assez imprécise. Lorsque la pièce était ronde ou profilée plutôt que carrée ou rectangulaire, la tâche de mesure devenait pratiquement impossible.
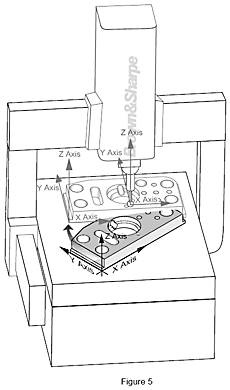
Le système de coordonnées : Qu’est-ce qu’un alignement ?
Avec le logiciel de MMT actuel, la MMT mesure les référentiels de pièces (à partir du plan de la pièce), établit le système de coordonnées de la pièce et l’associe mathématiquement au système de coordonnées de la machine.Le processus de mise en relation des deux systèmes de coordonnées s'appelle « alignement ». Si nous utilisons un plan de ville, nous le faisons automatiquement en tournant le plan de façon à ce qu’il soit parallèle à la rue (référentiel) ou à une direction de boussole (par ex. nord). Lorsque nous réalisons cela, nous nous localisons par rapport au « système de coordonnées du monde.

Qu’est-ce qu’un référentiel?
Un référentiel est un emplacement. Nous utilisons des référentiels comme guides pour indiquer aux autres où nous nous trouvons ou comme directions, signalant comment accéder à des destinations. Sur le plan, l’hôtel Ritz est un référentiel. C’est aussi le cas des rues, de la gare, du musée et du restaurant. Ainsi, en utilisant une origine, des référentiels, des directions et des distances, les personnes disposent de toutes les informations nécessaires pour aller d’un lieu à un autre.
Par exemple, pour aller de la gare (origine) au restaurant, vous parcourez 2 blocs vers le nord sur Elm Street (référentiel), prenez à droite, parcourez 2 blocs vers l’est sur Maple Street (référentiel).
Par exemple, pour aller de la gare (origine) au restaurant, vous parcourez 2 blocs vers le nord sur Elm Street (référentiel), prenez à droite, parcourez 2 blocs vers l’est sur Maple Street (référentiel).
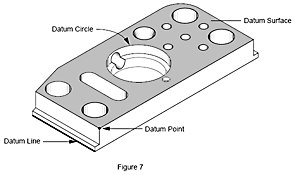
Dans le domaine de la métrologie, un référentiel est un élément sur une pièce, tel qu’un orifice, une surface ou un trou oblong. Nous mesurons une pièce pour déterminer la distance entre deux caractéristiques.
Qu’est-ce qu’une translation ?
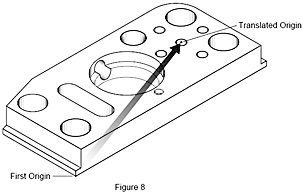
Supposons que vous deviez connaître la distance d’une entité donnée d’une pièce par rapport à une autre entité. Prenons, par exemple, la distance aux centres de chacun des quatre orifices à partir d’un trou central. Pour réaliser cela, nous commencerions par mesurer l’orifice central, puis nous effectuerions une translation de l’origine au centre de cet orifice, avant de mesurer chacun des quatre trous situés autour. Le déplacement du point de départ (origine) de la mesure à partir de la position actuelle vers une autre position sur la pièce s'appelle une translation. La MMT effectue cette translation de façon mathématique si vous activez une routine d'alignement dans son logiciel de mesure géométrique.
Pour en revenir à notre plan de ville, une fois arrivé à votre hôtel, si vous décidez de manger dans un restaurant réputé pendant votre visite, vous devez le localiser sur le plan. L’hôtel devient ainsi votre nouveau point de départ, ou origine. En connaissant votre emplacement, vous savez que vous devez parcourir deux blocs vers l’ouest sur Maple Street, pour atteindre le restaurant.
Pour en revenir à notre plan de ville, une fois arrivé à votre hôtel, si vous décidez de manger dans un restaurant réputé pendant votre visite, vous devez le localiser sur le plan. L’hôtel devient ainsi votre nouveau point de départ, ou origine. En connaissant votre emplacement, vous savez que vous devez parcourir deux blocs vers l’ouest sur Maple Street, pour atteindre le restaurant.
Qu’est-ce qu’une rotation ?
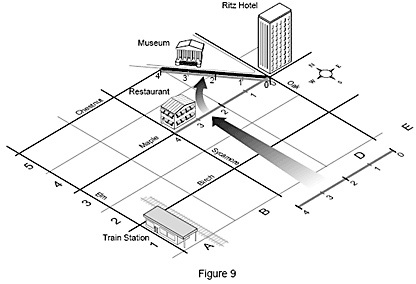
Tous les référentiels ne sont perpendiculaires à d'autres référentiels. Par exemple, si vous consultez votre plan, vous voyez que le musée se situe sur une rue qui n’est ni parallèle ni perpendiculaire aux rues de l’hôtel, du restaurant et de la gare. Ainsi, pour déterminer la distance entre l’hôtel et le musée, vous devez d'abord effectuer une translation de l’origine vers l’hôtel puis tourner le plan pour être parallèle à la rue où se trouve le musée. À présent, vous pouvez mesurer facilement la distance entre le musée et l’hôtel.
La même procédure s'applique à la pièce (figure 10). Il est possible de mesurer la distance entre deux orifices sur la pièce après la translation de l'origine initiale vers le plus petit orifice et la rotation mathématique du système de coordonnées pièce de 45°. Maintenant, les deux orifices se situent le long du nouvel axe Y et la distance est calculée automatiquement.
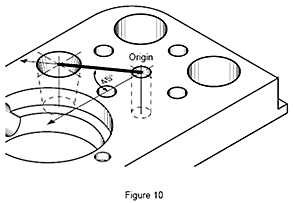
Entités mesurées et construites
Quelle est la différence entre des caractéristiques mesurées et construites ? La majorité des pièces sont formées d'éléments géométriques simples, réalisés par usinage ou formage. Ces unités primaires (plans, bords, cylindres, sphères, cônes, etc.) sont appelées « entités ». Lorsqu’une MMT mesure directement ces entités, en touchant les surfaces de l’entités avec un palpeur, on parle d’entités mesurées.
Il est impossible de mesurer directement d'autres caractéristiques, telles que la distance, la symétrie, l’intersection, l’angle et la projection. Il faut les construire mathématiquement à partir des entités mesurées pour déterminer leurs valeurs. On appelle ces entités des entités construites. Dans la figure 11, le cercle central est construit à partir des points de centre des quatre cercles mesurés.
Il est impossible de mesurer directement d'autres caractéristiques, telles que la distance, la symétrie, l’intersection, l’angle et la projection. Il faut les construire mathématiquement à partir des entités mesurées pour déterminer leurs valeurs. On appelle ces entités des entités construites. Dans la figure 11, le cercle central est construit à partir des points de centre des quatre cercles mesurés.
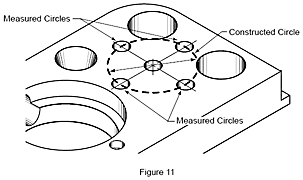
Entités construites
Les relations entre une entité ou un groupe d’entités par rapport à une autre entité ou un groupe d’entités sont critiques pour la fabrication. Par exemple, le point d’intersection entre les cylindres d'un côté d’un bloc-cylindres et ceux de l’autre côté détermine la qualité d'ajustement de pièces à assembler. Ce point d’intersection est construit à partir des deux entités mesurées (les cylindres du moteur).
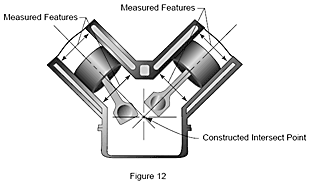
Qu’est-ce qu’une compensation volumétrique ?
Bien que la technologie de fabrication avancée permette de tolérancer et de réaliser des pièces de façon très précise, il existe toujours des imperfections. Aussi faibles qu’elles puissent être, le fait qu'il y ait des tolérances signifie qu'il y a des erreurs.
Les machines à mesurer tridimensionnelles ne se différencient pas d'autres produits à cet égard. Bien qu’elles soient construites sur la base de tolérances extrêmement étroites, il y a des erreurs (erreurs de roulis, de tangage, de lacet, de rectitude, de perpendicularité et d'échelle) qui affectent leur précision. Comme les tolérances de fabrication deviennent de plus en plus étroites, la précision des MMT doit augmenter.
L’ordinateur de la MMT peut corriger automatiquement la plupart des inexactitudes de la machine. Après la mesure de toutes les erreurs géométriques de la MMT (appelée « mappage d’erreurs »), leur minimisation, voire leur élimination, est possible au moyen d’algorithmes performants du logiciel de la MMT. Cette technique est appelée « compensation d’erreur volumétrique ».
L'élimination mathématique d’erreurs permet de réduire les coûts de fabrication et de fournir au client plus de performance pour le prix qu’il paie.
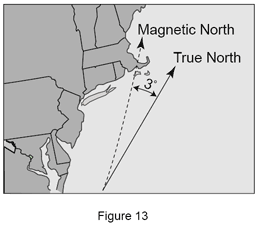
Pour expliquer ce qu’est une compensation volumétrique, nous allons prendre l’exemple d’une carte et d’une boussole. Si vous souhaitez naviguer vers un lieu donné, vous devez connaître la direction réelle à partir de votre position actuelle (origine). Nous utilisons une boussole et une carte pour déterminer votre direction, ou le gisement. Il y a cependant une différence entre le nord vrai et le nord magnétique. La différence entre les deux est appelée variation et est causée par la non-uniformité du champ magnétique terrestre. Ainsi, pour déterminer la direction vraie entre deux points, il faut ajouter la variation entre le nord vrai et le nord magnétique au gisement de la boussole ou l’en retirer.
Dans la carte illustrée, il faut compenser la différence entre le nord vrai et le nord magnétique (3° O), sinon un marin se trouverait au nord-ouest de la destination prévue et toucherait le fond avant d'atteindre la destination finale.
Une machine à mesurer tridimensionnelle effectue un type de compensation similaire en mode automatique pour supprimer les variations de la machine de la mesure.
Les machines à mesurer tridimensionnelles ne se différencient pas d'autres produits à cet égard. Bien qu’elles soient construites sur la base de tolérances extrêmement étroites, il y a des erreurs (erreurs de roulis, de tangage, de lacet, de rectitude, de perpendicularité et d'échelle) qui affectent leur précision. Comme les tolérances de fabrication deviennent de plus en plus étroites, la précision des MMT doit augmenter.
L’ordinateur de la MMT peut corriger automatiquement la plupart des inexactitudes de la machine. Après la mesure de toutes les erreurs géométriques de la MMT (appelée « mappage d’erreurs »), leur minimisation, voire leur élimination, est possible au moyen d’algorithmes performants du logiciel de la MMT. Cette technique est appelée « compensation d’erreur volumétrique ».
L'élimination mathématique d’erreurs permet de réduire les coûts de fabrication et de fournir au client plus de performance pour le prix qu’il paie.
Pour expliquer ce qu’est une compensation volumétrique, nous allons prendre l’exemple d’une carte et d’une boussole. Si vous souhaitez naviguer vers un lieu donné, vous devez connaître la direction réelle à partir de votre position actuelle (origine). Nous utilisons une boussole et une carte pour déterminer votre direction, ou le gisement. Il y a cependant une différence entre le nord vrai et le nord magnétique. La différence entre les deux est appelée variation et est causée par la non-uniformité du champ magnétique terrestre. Ainsi, pour déterminer la direction vraie entre deux points, il faut ajouter la variation entre le nord vrai et le nord magnétique au gisement de la boussole ou l’en retirer.
Dans la carte illustrée, il faut compenser la différence entre le nord vrai et le nord magnétique (3° O), sinon un marin se trouverait au nord-ouest de la destination prévue et toucherait le fond avant d'atteindre la destination finale.
Une machine à mesurer tridimensionnelle effectue un type de compensation similaire en mode automatique pour supprimer les variations de la machine de la mesure.
Qualification des pointes de palpeur Compensation de palpeur
Les MMT acquièrent en général des données en touchant la pièce avec un palpeur (physique ou à déclenchement point par point électronique) fixé sur l'axe de mesure de la machine. Bien que la pointe du palpeur soit très précise, une fois que le palpeur est fixé à la MMT, il faut déterminer l’emplacement de la pointe par rapport au système de coordonnées de la machine avant la mesure. Comme la circonférence de la pointe touche la pièce, le centre du palpeur et son rayon sont déterminés par la mesure d'une sphère très précise (sphère de requalification).
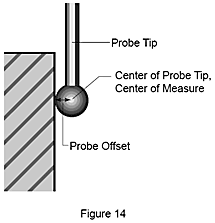
Une fois que le centre et le rayon de la pointe sont connus, lorsque le palpeur touche une pièce, les coordonnées de la pointe sont décalées mathématiquement du rayon de la pointe vers le point de contact effectif de la pointe (figure 14). La direction du décalage est déterminée de façon automatique par la procédure d'alignement.
Nous appliquons une procédure similaire lorsque nous garons un véhicule. Plus la qualité de l’estimation à partir de l’extérieur du véhicule est haute, mieux nous pouvons garer la voiture près du trottoir.
Une fois que le centre et le rayon de la pointe sont connus, lorsque le palpeur touche une pièce, les coordonnées de la pointe sont décalées mathématiquement du rayon de la pointe vers le point de contact effectif de la pointe (figure 14). La direction du décalage est déterminée de façon automatique par la procédure d'alignement.
Nous appliquons une procédure similaire lorsque nous garons un véhicule. Plus la qualité de l’estimation à partir de l’extérieur du véhicule est haute, mieux nous pouvons garer la voiture près du trottoir.
Projections
Une projection est la reproduction d’une caractéristique de pointe sur une autre caractéristique, par exemple la projection d’un cercle ou d'une ligne sur un plan, ou d’un point sur une ligne.
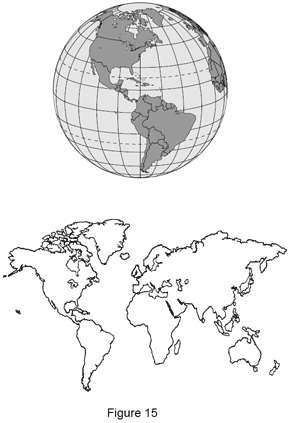
On peut comparer la projection d’une entité de la pièce sur une autre avec la création de la carte « plane » classique du monde (projection Mercator). La carte plane résulte de la projection d'un globe du monde (sphère) sur un cylindre.
On peut comparer la projection d’une entité de la pièce sur une autre avec la création de la carte « plane » classique du monde (projection Mercator). La carte plane résulte de la projection d'un globe du monde (sphère) sur un cylindre.
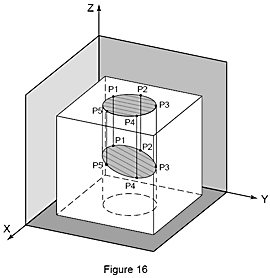
Dans le domaine de la métrologie, les projections vous permettent de mesurer avec plus de précision la façon dont les pièces à assembler seront ajustées. Dans le cadre des mesures des cylindres de voiture (par ex. blocs-cylindres), en projetant un cylindre sur le plan de la face de tête, vous pouvez déterminer de façon précise comment les pistons sont ajustés au cylindre et comment la tête cadre avec la chambre de combustion.
Un nombre minimum de trois points est nécessaire pour mesurer le diamètre d’un cercle et, si ces points ne sont pas placés à la même distance de la partie supérieure de l'alésage, le diamètre mesuré aura une forme elliptique. Pour éliminer cette erreur de représentation, les données mesurées sont projetées sur un plan perpendiculaire à l’axe du cylindre. Le résultat est une détermination précise de la taille réelle de cette caractéristique de pièce.
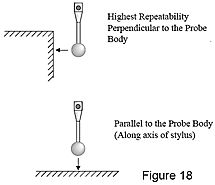
Il convient par exemple d’effectuer les mesures par palpeur perpendiculairement à la surface de la pièce si cela est possible. Les palpeurs à déclenchement point par point utilisés sur les machines à mesurer tridimensionnelles sont conçus pour donner des résultats optimaux lorsque la pointe du palpeur touche la pièce perpendiculairement au corps du palpeur. Idéalement, il faudrait effectuer des palpages dans une plage de ± 20° de l’axe perpendiculaire pour éviter un glissement de la pointe. Un glissement provoque des résultats incohérents, non répétables.
Un nombre minimum de trois points est nécessaire pour mesurer le diamètre d’un cercle et, si ces points ne sont pas placés à la même distance de la partie supérieure de l'alésage, le diamètre mesuré aura une forme elliptique. Pour éliminer cette erreur de représentation, les données mesurées sont projetées sur un plan perpendiculaire à l’axe du cylindre. Le résultat est une détermination précise de la taille réelle de cette caractéristique de pièce.

Application de techniques de palpage efficaces
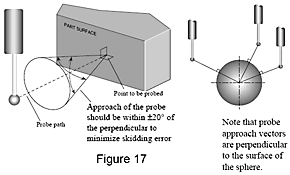
À l’aide de techniques de palpage efficaces lors de l’inspection d'une pièce, vous pouvez éliminer de nombreuses causes courantes d’erreur de mesure.Il convient par exemple d’effectuer les mesures par palpeur perpendiculairement à la surface de la pièce si cela est possible. Les palpeurs à déclenchement point par point utilisés sur les machines à mesurer tridimensionnelles sont conçus pour donner des résultats optimaux lorsque la pointe du palpeur touche la pièce perpendiculairement au corps du palpeur. Idéalement, il faudrait effectuer des palpages dans une plage de ± 20° de l’axe perpendiculaire pour éviter un glissement de la pointe. Un glissement provoque des résultats incohérents, non répétables.
Surface de pièce à palper
À noter que l'approche du palpeur doit se trouver dans une plage de ±20° par rapport à l’axe perpendiculaire pour réduire au maximum l’erreur de glissement. Les vecteurs d'approche du palpeur sont perpendiculaires à la surface de la sphère.
Application de techniques de palpage efficaces
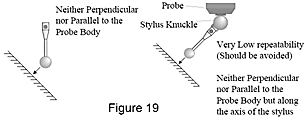
Les palpages qui ne sont ni perpendiculaires ni parallèles au corps de palpeur (figure 19) produisent des résultats encore moins répétables que les palpages parallèles au corps. Il convient d’éviter des palpages parallèles au stylet et effectués à un certain angle par rapport au corps du palpeur, car ils aboutissent à de grandes erreurs.
Application de techniques de palpage efficaces
Vous pouvez réduire le risque d'un contact avec la tige en utilisant une pointe de plus grand diamètre pour augmenter l’espace entre la boule/tige et la surface de la pièce. En général, plus le diamètre de la pointe est grand, plus le stylet peut s’abaisser avant de toucher l’entité de la pièce. On désigne ce paramètre par longueur de travail utile du palpeur (figure 21). Par ailleurs, plus la pointe est grande, plus l’effet sur la finition de la surface de la pièce est réduit, étant donné que le point de contact est distribué sur une plus grande zone de l’entité à mesurer. Mais, la plus grande pointe utilisable est limitée par la taille des plus petits orifices à mesurer.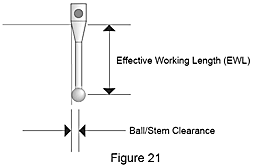
Les points mesurés avec un palpeur électronique sont enregistrés lorsque le stylet est suffisamment solide pour casser les contacts mécaniques ou générer assez de force pour déclencher un circuit sensible à la pression. La disposition physique des contacts cause de petites erreurs de précision, bien que celles-ci soient réduites pendant la qualification du palpeur. Cependant, plus la rallonge du palpeur est longue, plus l’erreur de précourse est importante et plus l’erreur résiduelle est grande après la qualification du palpeur. Les palpeurs longs sont moins rigides que les palpeurs plus courts. Plus le stylet se courbe ou dévie, plus l’imprécision est élevée. Il convient d'éviter d’utiliser des palpeurs ayant de très longues combinaisons stylet/rallonge.
 On utilise des formes, appelées éléments géométriques, pour définir une pièce et ses caractéristiques. Ces formes sont : le point, la ligne, le plan, le cercle, le cylindre, le cône et la sphère. Il y a aussi des entités géométriques qui déterminent l'état des pièces et la relation des entités.
On utilise des formes, appelées éléments géométriques, pour définir une pièce et ses caractéristiques. Ces formes sont : le point, la ligne, le plan, le cercle, le cylindre, le cône et la sphère. Il y a aussi des entités géométriques qui déterminent l'état des pièces et la relation des entités.
Ces symboles géométriques sont similaires aux symboles utilisés sur les cartes pour indiquer des éléments comme des autoroutes à deux ou quatre voies, des ponts, des aéroports. Ils sont comme les nouveaux signes de circulation internationaux vus sur les autoroutes américaines. Le but de ces symboles est de former un langage commun que tout le monde peut comprendre.
Dimensionnement et tolérancement géométrique
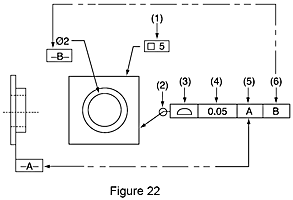
Le dimensionnement et tolérancement géométrique (GD&T) est un langage universel de symboles, un peu comme le système international des panneaux de circulation qui guide les conducteurs lors du déplacement sur des routes. Les symboles GD&T permettent à un ingénieur de conception de décrire de façon précise et logique des entités de pièce afin qu'il soit possible de les fabriquer et les inspecter de façon précise. Les données GD&T figurent dans le cadre de référence de l’entité. Le contrôle de référence de l’entité ressemble à une phrase rudimentaire que l’on peut lire de gauche à droite. Le cadre de référence de l’entité illustré, par exemple, signifierait la chose suivante : la forme carrée de 5 mm (1) est associée à une tolérance de profil (3) sur toutes les faces (2) de 0,05 mm (4), en relation avec le référentiel primaire A (5) et le référentiel secondaire B (6). La forme et la tolérance déterminent les limites de la variabilité de production.
Ces symboles géométriques sont similaires aux symboles utilisés sur les cartes pour indiquer des éléments comme des autoroutes à deux ou quatre voies, des ponts, des aéroports. Ils sont comme les nouveaux signes de circulation internationaux vus sur les autoroutes américaines. Le but de ces symboles est de former un langage commun que tout le monde peut comprendre.
Symboles d’entités géométriques
- Rectitude — état dans lequel tous les points se trouvent sur une ligne droite, la tolérance étant spécifiée par une zone formée de deux lignes parallèles.
- Planéité — tous les points se trouvent sur un plan, la tolérance étant spécifiée par une zone formée de deux plans parallèles.
- Rotondité ou circularité — tous les points sur une surface se trouvent dans un cercle. La tolérance est spécifiée par une zone bordée de deux cercles concentriques.
- Cylindricité — tous les points d’une surface de révolution sont équidistants par rapport à un axe commun. Une tolérance de cylindricité spécifie une zone de tolérance bordée par deux cylindres concentriques à l’intérieur desquels la surface doit se trouver.
- Profil — une méthode de tolérancement pour contrôler des surfaces irrégulières, lignes, arcs ou plans standard. On peut appliquer des profils sur des éléments de ligne individuels ou sur toute la surface d'une pièce. La tolérance de profil spécifie une limite uniforme le long du profil vrai à l’intérieur duquel les éléments de la surface doivent se trouver.
- Angularité — état d’une surface ou d’un axe à un angle spécifié (autre que 90°) à partir d'un plan ou axe de référence. La zone de tolérance est définie par deux plans parallèles à l'angle de base spécifié à partir d'un plan ou axe de référence.
- Perpendicularité — état d’une surface ou d’un axe perpendiculaire à un plan ou axe de référence. La tolérance de perpendicularité spécifie : une zone définie par deux plans perpendiculaires à un plan ou axe de référence, ou une zone définie par deux plans parallèles perpendiculaires à l’axe de référence.
- Parallélisme — état d’une surface ou d’un axe équidistant à tous les points d’un plan ou axe de référence. La tolérance de parallélisme spécifie : une zone définie par deux plans ou lignes parallèles à un plan ou axe de référence, ou une zone de tolérance cylindrique dont l’axe est parallèle à un axe de référence.
- Concentricité — les axes de tous les éléments de profil en travers d'une surface de révolution sont communs à l'axe de la caractéristique de référence. La tolérance de concentricité spécifie une zone de tolérance cylindrique dont l’axe coïncide avec l’axe de référence.
- Position — une tolérance de position définit une zone dans laquelle l’axe central ou le plan central peut varier par rapport à la position réelle (théoriquement exacte). Les dimensions de base établissent la position vraie à partir des entités de référence et entre les entités corrélées. Une tolérance de position est la variation totale admissible en position d'une entité par rapport à sa position exacte. Pour les entités cylindriques telles que les orifices et diamètres extérieurs, la tolérance de position est en général le diamètre de la zone de tolérance dans laquelle l’axe de l’entité doit se situer. Pour les entités qui ne sont pas rondes, telles que les trous oblongs et les languettes, la tolérance de position est la largeur totale de la zone de tolérance dans le plan central de l’entité doit se situer.
- Faux-rond — permet de contrôler les éléments circulaires d'une surface. La tolérance est appliquée de façon indépendante à chaque position de mesure circulaire, la pièce étant tournée de 360 degrés. Une tolérance de faux-rond appliquée à des surfaces construite autour d’un axe de référence contrôle les variations cumulées de la circularité et de la coaxialité. Lorsqu’elle est appliquée à des surfaces perpendiculaires à l’axe de référence, elle contrôle les éléments circulaires d'un plan.
- Battement total — permet un contrôle combiné de tous les éléments de surface. La tolérance est appliquée simultanément aux éléments circulaires et longitudinaux, la pièce étant tournée de 360 degrés. Le battement total contrôle la variation cumulée de la circularité, de la cylindricité, de la linéarité, de la coaxialité, l’angularité, la conicité et du profil, lorsqu'il est appliqué à des surfaces construites autour d’un axe de référence. Lorsqu’il est appliqué à des surfaces perpendiculaires à un axe de référence, il contrôle les variations cumulées de perpendicularité et de planéité.
