Úvod do souřadnicového měření
Princip SMS: Souřadnicový systém.
Kontakty
Souřadnicový systém používáme k popisu pohybu měřicího stroje. Souřadnicový systém, vynalezený slavným francouzským filozofem a matematikem René Descartesem na začátku 17. století, nám umožňuje lokalizovat prvky na výrobcích ve vztahu k jiným prvkům.
Souřadnicový systém je něco jako topografická mapa, ve které kombinace písmena u jednoho okraje mapy, čísla u druhého okraje a nadmořské výšky zobrazené na ploše mapy jednoznačně popisuje každé místo na mapě. Tato kombinace písmena/čísla/nadmořské výšky se nazývá souřadnice a zastupuje konkrétní místo ve vztahu ke všem ostatním.
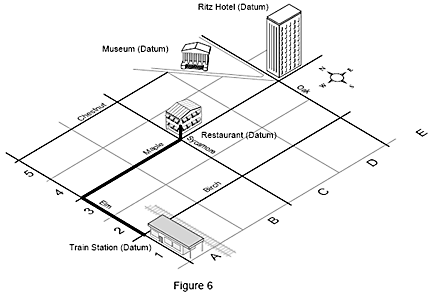
Dalším příkladem je mapa ulic s budovami. Chcete-li dojít do svého hotelového pokoje v hotelu Ritz z vlakového nádraží (počátek vaší cesty), musíte jít 2 bloky po Elm street, 4 bloky po Maple a potom vystoupat tři patra v hotelu Ritz. Toto místo lze rovněž popsat souřadnicemi 4-E-3 na mapě, což odpovídá osám X, Y a Z ve stroji. Tyto souřadnice jednoznačně popisují váš pokoj a žádné jiné místo na mapě.
Souřadnicový měřicí stroj (SMS) pracuje podobně, jako když sledujete prstem na mapě souřadnice - to jsou tři osy souřadnicového systému stroje. Místo prstu používá SMS k měření bodů na výrobku sondu. Každý bod na výrobku je v souřadnicovém systému stroje jedinečný. SMS kombinuje naměřené body dohromady a vytvoří prvek, který můžete vztáhnout k jiným prvkům.
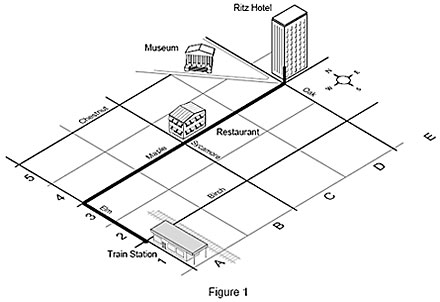
Souřadnicový systém je něco jako topografická mapa, ve které kombinace písmena u jednoho okraje mapy, čísla u druhého okraje a nadmořské výšky zobrazené na ploše mapy jednoznačně popisuje každé místo na mapě. Tato kombinace písmena/čísla/nadmořské výšky se nazývá souřadnice a zastupuje konkrétní místo ve vztahu ke všem ostatním.
Dalším příkladem je mapa ulic s budovami. Chcete-li dojít do svého hotelového pokoje v hotelu Ritz z vlakového nádraží (počátek vaší cesty), musíte jít 2 bloky po Elm street, 4 bloky po Maple a potom vystoupat tři patra v hotelu Ritz. Toto místo lze rovněž popsat souřadnicemi 4-E-3 na mapě, což odpovídá osám X, Y a Z ve stroji. Tyto souřadnice jednoznačně popisují váš pokoj a žádné jiné místo na mapě.
Souřadnicový měřicí stroj (SMS) pracuje podobně, jako když sledujete prstem na mapě souřadnice - to jsou tři osy souřadnicového systému stroje. Místo prstu používá SMS k měření bodů na výrobku sondu. Každý bod na výrobku je v souřadnicovém systému stroje jedinečný. SMS kombinuje naměřené body dohromady a vytvoří prvek, který můžete vztáhnout k jiným prvkům.


Souřadnicový systém: Souřadnicový systém stroje
Ve světě měření existují dva typy souřadnicových systémů. První se nazývá souřadnicový systém stroje. V něm osy X, Y a Z odpovídají na pohybu stroje. Při pohledu na stroj zepředu probíhá osa X zleva doprava, osa Y zepředu dozadu a osa Z shora dolů, je tedy kolmá na ostatní dvě.
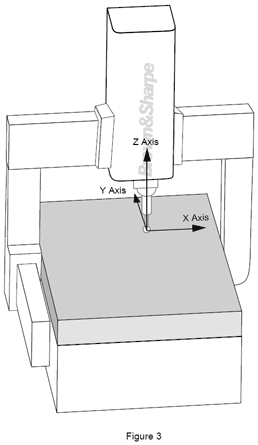

Souřadnicový systém: Souřadnicový systém dílu
Druhý souřadnicový systém se nazývá souřadnicový systém dílu, ve kterém jsou tři osy vztaženy k údajům nebo prvkům výrobku.
Než byl do souřadnicového měření zaveden počítačový software, díly se fyzicky vyrovnaly s osami stroje tak, aby byly souřadnicové systémy stroje a dílu paralelní. Bylo to velmi časově náročné a nepříliš přesné. Když nebyl díl čtvercový nebo obdélníkový, ale zaoblený nebo tvarovaný, měření bylo téměř nemožné.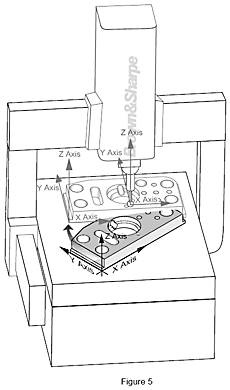
Než byl do souřadnicového měření zaveden počítačový software, díly se fyzicky vyrovnaly s osami stroje tak, aby byly souřadnicové systémy stroje a dílu paralelní. Bylo to velmi časově náročné a nepříliš přesné. Když nebyl díl čtvercový nebo obdélníkový, ale zaoblený nebo tvarovaný, měření bylo téměř nemožné.

Souřadnicový systém: Co je vyrovnání?
S pomocí současného softwaru změří SMS základny výrobku (určené výkresem dílu), vytvoří souřadnicový systém a matematicky ho vztáhne k souřadnicovému systému stroje.
Proces vztažení dvou souřadnicových systémů se nazývá vyrovnání. S mapou ulic to uděláme tím způsobem, že automaticky otočíme mapu tak, aby byla paralelně s ulicí (údajem) nebo se směrem udaným kompasem (tj. severem). Když to uděláme, umístíme sami sebe do „souřadnicového systému světa“.
Například chcete-li se dostat z vlakového nádraží (počátek) do restaurace, půjdete 2 bloky na sever po Elm Street (základna), dáte se doprava a půjdete 2 bloky na východ po Maple (základna).
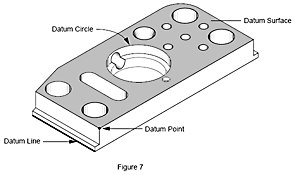
 V metrologii je základna prvek na výrobku, například otvor, povrch nebo drážka. Výrobek měříme, abychom zjistili vzdálenost od jednoho prvku k druhému.
V metrologii je základna prvek na výrobku, například otvor, povrch nebo drážka. Výrobek měříme, abychom zjistili vzdálenost od jednoho prvku k druhému.
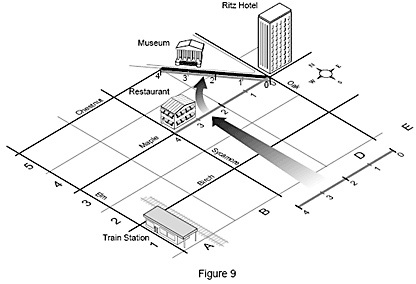
Když použijeme mapu ulic, tak jakmile dorazíte do hotelu a rozhodnete se, že se cestou do města najíte v legendární restauraci, musíte ji najít na mapě. Hotel se nyní stává novým počátečním bodem, neboli počátkem. Když znáte svou polohu, pohledem na mapu dokážete určit, že do restaurace se dostanete, když půjdete dva bloky na západ po Maple Street.
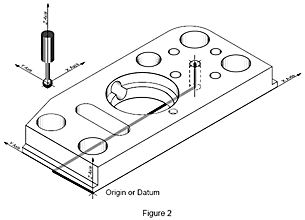
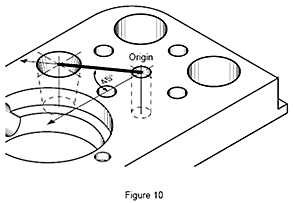
 Přesně stejný postup platí pro výrobek (obr. 10). Vzdálenost mezi dvěma otvory na výrobku lze změřit v okamžiku, kdy přeneseme počátek do menšího otvoru a souřadnicový systém dílu se matematicky otočí o 45°. Nyní se oba otvory nachází podél nové osy Y a vzdálenost lze automaticky spočítat.
Přesně stejný postup platí pro výrobek (obr. 10). Vzdálenost mezi dvěma otvory na výrobku lze změřit v okamžiku, kdy přeneseme počátek do menšího otvoru a souřadnicový systém dílu se matematicky otočí o 45°. Nyní se oba otvory nachází podél nové osy Y a vzdálenost lze automaticky spočítat.
Jiné prvky, například vzdálenosti, symetrie, průsečíky, úhly a průměty nelze měřit přímo, ale musí se zkonstruovat matematicky z předtím naměřených prvků. Proto je nazýváme konstruované prvky. Na obr. 11 je středová kružnice zkonstruována ze středů čtyř změřených kružnic.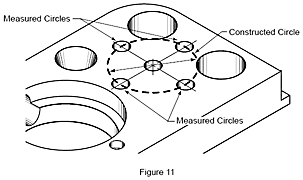
Souřadnicové měřicí stroje se v tomto směru nijak neliší od ostatních produktů. I když jsou vyráběny s mimořádně přísnými tolerancemi, v jejich konstrukci se vyskytují chyby (valivé, rozteče, výkyvu, přímosti, čtvercovosti a měřítek), které ovlivňují jejich přesnost. Protože jsou výrobní tolerance čím dál tím striktnější, je nezbytné, aby byly SMS stále přesnější.
Většinu nepřesností SMS lze automaticky opravit v kontroléru SMS. Když jsou změřeny všechny geometrické chyby SMS (tzv. mapování), dají se minimalizovat nebo eliminovat pomocí výkonných algoritmů softwaru SMS. Tato metoda se nazývá volumetrická kompenzace chyb.
Matematickou eliminací chyb snížíte výrobní náklady a poskytnete zákazníkovi za jeho peníze lepší přesnost.
Volumetrická kompenzace se nejlépe vysvětluje pomocí vztahu mezi mapou a kompasem. Pokud se chcete dopravit na určité místo, musíte znát správný směr ze své současné pozice (počátku). Kompas a mapa se používají k určení vašeho směru. Existuje ovšem rozdíl mezi skutečným severem a magnetickým severem. Tento rozdíl se nazývá odchylka a je způsobena nestejnorodostí zemského magnetického pole. Pro určení správného směru z jednoho bodu do druhého je tudíž nutno k údaji kompasu přičíst (nebo od něho odečíst) rozdíl mezi skutečným a magnetickým severem.
Na zobrazené mapě je nutné vykompenzovat rozdíl mezi skutečným a magnetickým severem (3° W), protože jinak by námořník skončil severozápadně od zamýšleného cíle a narazil by na souš předtím, než by doplul do cíle.
Souřadnicový měřicí stroj automaticky provádí podobnou kompenzaci, aby eliminoval chyby stroje od naměřených hodnot.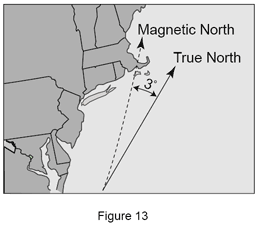
Jakmile známe střed a poloměr kuličky, v okamžiku, kdy se sonda dotkne výrobku, posunou se souřadnice kuličky matematicky do skutečného bodu kontaktu o poloměr kuličky (obr. 14). Směr posunu se automaticky určí postupem vyrovnání.
Podobně postupujeme při parkování auta. Čím lépe odhadneme náš odstup od auta, tím blíže k chodníku zaparkujeme.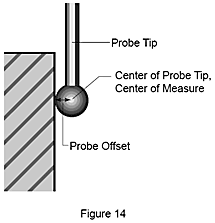
Průmět jednoho prvku dílu na jiný lze ilustrovat vytvořením tradiční „ploché“ mapy světa (Mercatorova projekce). Plochá mapa se vytvoří promítnutím zeměkoule (koule) na válec.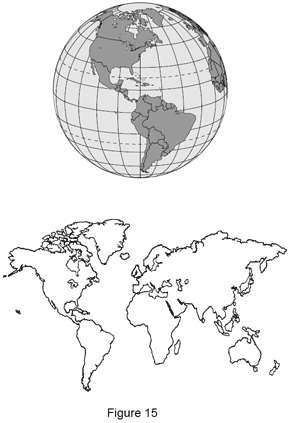 V metrologii průmět umožňuje přesněji změřit, jak spolu budou protikusy skutečně lícovat. Při měření automobilových válců (např. bloků motoru) můžete promítnutím válce do roviny čela hlavy přesněji určit, jak se písty vejdou do válce a jak budou lícovat se spalovací komorou hlavy.
V metrologii průmět umožňuje přesněji změřit, jak spolu budou protikusy skutečně lícovat. Při měření automobilových válců (např. bloků motoru) můžete promítnutím válce do roviny čela hlavy přesněji určit, jak se písty vejdou do válce a jak budou lícovat se spalovací komorou hlavy.
Ke změření průměru kružnice potřebujeme nejméně tři body, a pokud tyto body nejsou ve stejné vzdálenosti od horní úrovně vývrtu, naměřený průměr bude zobrazen jako eliptický. Aby se zabránilo této dezinterpretaci, naměřená data se promítnou do roviny kolmé na osu válce. Výsledkem je přesné stanovení skutečné velikosti výrobku.
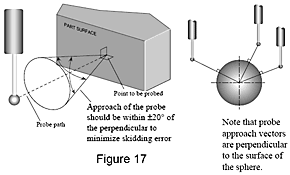
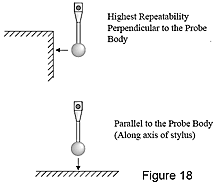
Např. dotek by se měl povrchu výrobku dotýkat kolmo, kdykoli je to možné. Dotykové spínací sondy používané u souřadnicových měřicích strojů jsou navrženy tak, aby poskytovaly optimální výsledky, když se kulička doteku dotýká výrobku kolmo na povrch výrobku. V ideálním případě byste měli měřit při sklonu v rozmezí ±20° od kolmice, aby nedošlo ke sklouznutí kuličky doteku. Sklouznutí produkuje nekonzistentní, neopakovatelné výsledky.
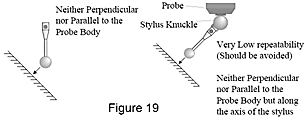 Další příčinou chyb měření je dotek dříkem (obr. 20). Když se sonda dotkne výrobku dříkem doteku a nikoli kuličkou, měřicí systém se domnívá, že měření bylo provedeno normálním způsobem a vzniknou velké chyby.
Další příčinou chyb měření je dotek dříkem (obr. 20). Když se sonda dotkne výrobku dříkem doteku a nikoli kuličkou, měřicí systém se domnívá, že měření bylo provedeno normálním způsobem a vzniknou velké chyby.
 Měřené body pořízené sondou se zaznamenají, když se dotek odchýlí natolik, aby buď rozpojil mechanické kontakty, nebo vygeneroval dostatečnou sílu ke spuštění obvodu citlivého na tlak. Fyzické uspořádání kontaktů sondy má negativní vliv na přesnost, přestože jsou tyto chyby značně redukovány během kalibrace sondy. Nicméně čím delší je prodlužovací nástavec kuličky doteku, tím větší je počáteční chyba a tím větší chyba zůstane po kalibraci sondy. Delší sondy nejsou tak pevné jako kratší. Čím více se dotek ohýbá nebo vychyluje, tím nižší je přesnost. Nepoužívejte sondy s velmi dlouhou kombinací dotek/prodlužovací nástavec.
Měřené body pořízené sondou se zaznamenají, když se dotek odchýlí natolik, aby buď rozpojil mechanické kontakty, nebo vygeneroval dostatečnou sílu ke spuštění obvodu citlivého na tlak. Fyzické uspořádání kontaktů sondy má negativní vliv na přesnost, přestože jsou tyto chyby značně redukovány během kalibrace sondy. Nicméně čím delší je prodlužovací nástavec kuličky doteku, tím větší je počáteční chyba a tím větší chyba zůstane po kalibraci sondy. Delší sondy nejsou tak pevné jako kratší. Čím více se dotek ohýbá nebo vychyluje, tím nižší je přesnost. Nepoužívejte sondy s velmi dlouhou kombinací dotek/prodlužovací nástavec.
 Existuje sedm tvarů, nazývaných geometrické prvky, které se používají k definování dílu a jeho prvků. Jsou to následující tvary: bod, přímka, rovina, kružnice, válec, kužel a koule. Existují také určité geometrické charakteristiky, které určují stav dílů a vztahy mezi prvky.
Existuje sedm tvarů, nazývaných geometrické prvky, které se používají k definování dílu a jeho prvků. Jsou to následující tvary: bod, přímka, rovina, kružnice, válec, kužel a koule. Existují také určité geometrické charakteristiky, které určují stav dílů a vztahy mezi prvky.
Tyto geometrické symboly se podobají symbolům používaným v mapách k označení prvků, např. dvouproudových a čtyřproudových dálnic, mostů a letišť. Podobají se novým mezinárodním dopravním značkám, které jsou častěji vidět na amerických dálnicích. Účelem těchto symbolů je také vytvořit společný jazyk, kterému bude každý rozumět.
Proces vztažení dvou souřadnicových systémů se nazývá vyrovnání. S mapou ulic to uděláme tím způsobem, že automaticky otočíme mapu tak, aby byla paralelně s ulicí (údajem) nebo se směrem udaným kompasem (tj. severem). Když to uděláme, umístíme sami sebe do „souřadnicového systému světa“.

Co je to základna?
Základna je poloha. Základny používáme jako vodítka, abychom sdělili ostatním, kde jsme, nebo k určení směrů, jak se dostat na daná místa. Na mapě je základnou Hotel Ritz. Stejně jako ulice, vlakové nádraží, muzeum a restaurace. Pomocí počátku, základen, směrů a vzdáleností tak lidé získají všechny informace, které potřebují, aby se dostali z jednoho místa na druhé.Například chcete-li se dostat z vlakového nádraží (počátek) do restaurace, půjdete 2 bloky na sever po Elm Street (základna), dáte se doprava a půjdete 2 bloky na východ po Maple (základna).


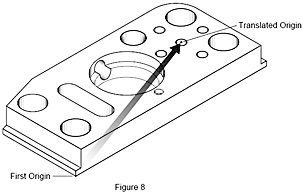
Co je translace?
Předpokládejme, že potřebujete vědět, jak daleko je konkrétní prvek na výrobku od jiného prvku. Vezměme například vzdálenost středů čtyř otvorů od středového otvoru. K tomu musíte nejprve změřit středový otvor, přenést počátek do středu tohoto otvoru a potom změřit čtyři okolní otvory. Přesunutí počátečního bodu (počátku) měření ze současné pozice na jiné místo na výrobku se nazývá translace. SMS ho provádí matematicky, když si v softwaru pro měření geometrie vyžádáte program pro vyrovnání.Když použijeme mapu ulic, tak jakmile dorazíte do hotelu a rozhodnete se, že se cestou do města najíte v legendární restauraci, musíte ji najít na mapě. Hotel se nyní stává novým počátečním bodem, neboli počátkem. Když znáte svou polohu, pohledem na mapu dokážete určit, že do restaurace se dostanete, když půjdete dva bloky na západ po Maple Street.

Co je rotace?
Ne všechny údaje jsou vůči jiným údajům v pravých úhlech. Když se například podíváte na mapu a vidíte, že muzeum je v ulici, která není rovnoběžná ani kolmá vůči ulicím s hotelem, restaurací a vlakovým nádražím. Když tedy chcete určit, jak daleko je z hotelu do muzea, musíte nejprve přenést počátek souřadnic do hotelu a potom ho otočit tak, aby byl rovnoběžně s ulicí, ve které je muzeum. Nyní můžete snadno změřit vzdálenost od muzea k hotelu.

Měřené a konstruované prvky
Jaký je rozdíl mezi měřenými a konstruovanými prvky? Velká většina výrobků se skládá z jednoduchých geometrických elementů, vytvořených obráběním nebo tvářením. Tyto primární elementy (roviny, hrany, válce, koule, kužele atd.) se nazývají prvky. Když SMS dokáže tyto prvky přímo změřit tím, že se dotkne povrchu dotekem, nazývají se měřené prvky.Jiné prvky, například vzdálenosti, symetrie, průsečíky, úhly a průměty nelze měřit přímo, ale musí se zkonstruovat matematicky z předtím naměřených prvků. Proto je nazýváme konstruované prvky. Na obr. 11 je středová kružnice zkonstruována ze středů čtyř změřených kružnic.

Konstrukční prvky
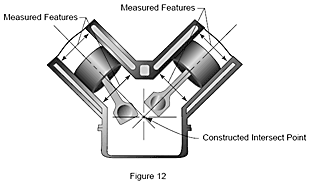
Vztah mezi jedním prvkem nebo skupinou prvků a jiným prvkem nebo skupinou prvků je pro výrobu kritický. Například průsečík mezi válci na jedné straně bloku motoru a na druhé straně určuje, jak budou k sobě díly pasovat. Tento průsečík je zkonstruován ze dvou změřených prvků (válců motoru).

Co je to volumetrická kompenzace?
Přestože moderní výrobní technologie umožňují dodržovat velmi přísné tolerance a vyrábět velmi přesné výrobky, stále se vyskytují nedokonalosti. Ať jsou sebemenší, skutečnost, že existují tolerance znamená, že existují chyby.Souřadnicové měřicí stroje se v tomto směru nijak neliší od ostatních produktů. I když jsou vyráběny s mimořádně přísnými tolerancemi, v jejich konstrukci se vyskytují chyby (valivé, rozteče, výkyvu, přímosti, čtvercovosti a měřítek), které ovlivňují jejich přesnost. Protože jsou výrobní tolerance čím dál tím striktnější, je nezbytné, aby byly SMS stále přesnější.
Většinu nepřesností SMS lze automaticky opravit v kontroléru SMS. Když jsou změřeny všechny geometrické chyby SMS (tzv. mapování), dají se minimalizovat nebo eliminovat pomocí výkonných algoritmů softwaru SMS. Tato metoda se nazývá volumetrická kompenzace chyb.
Matematickou eliminací chyb snížíte výrobní náklady a poskytnete zákazníkovi za jeho peníze lepší přesnost.
Volumetrická kompenzace se nejlépe vysvětluje pomocí vztahu mezi mapou a kompasem. Pokud se chcete dopravit na určité místo, musíte znát správný směr ze své současné pozice (počátku). Kompas a mapa se používají k určení vašeho směru. Existuje ovšem rozdíl mezi skutečným severem a magnetickým severem. Tento rozdíl se nazývá odchylka a je způsobena nestejnorodostí zemského magnetického pole. Pro určení správného směru z jednoho bodu do druhého je tudíž nutno k údaji kompasu přičíst (nebo od něho odečíst) rozdíl mezi skutečným a magnetickým severem.
Na zobrazené mapě je nutné vykompenzovat rozdíl mezi skutečným a magnetickým severem (3° W), protože jinak by námořník skončil severozápadně od zamýšleného cíle a narazil by na souš předtím, než by doplul do cíle.
Souřadnicový měřicí stroj automaticky provádí podobnou kompenzaci, aby eliminoval chyby stroje od naměřených hodnot.

Kompenzace kuličky doteku
SMS obecně shromažďují data tak, že se dotýkají výrobku dotekem připevněným na měřicí ose stroje. Přestože je kulička doteku velmi přesná, jakmile se dotek připojí k SMS, je nutné před měřením stanovit polohu středu kuličky v souřadnicovém systému stroje. Protože se dílu dotýká obvod kuličky, střed a poloměr sondy se určí změřením velmi přesné kalibrační koule.Jakmile známe střed a poloměr kuličky, v okamžiku, kdy se sonda dotkne výrobku, posunou se souřadnice kuličky matematicky do skutečného bodu kontaktu o poloměr kuličky (obr. 14). Směr posunu se automaticky určí postupem vyrovnání.
Podobně postupujeme při parkování auta. Čím lépe odhadneme náš odstup od auta, tím blíže k chodníku zaparkujeme.

Průmět
Průmět je reprodukce prvku výrobku na jiný prvek, například projekce kružnice nebo přímky do roviny, nebo bodu na přímku.Průmět jednoho prvku dílu na jiný lze ilustrovat vytvořením tradiční „ploché“ mapy světa (Mercatorova projekce). Plochá mapa se vytvoří promítnutím zeměkoule (koule) na válec.

Ke změření průměru kružnice potřebujeme nejméně tři body, a pokud tyto body nejsou ve stejné vzdálenosti od horní úrovně vývrtu, naměřený průměr bude zobrazen jako eliptický. Aby se zabránilo této dezinterpretaci, naměřená data se promítnou do roviny kolmé na osu válce. Výsledkem je přesné stanovení skutečné velikosti výrobku.

Použití účinných metod dotekového měření
Pomocí účinných metod dotekového měření při kontrole výrobku je možné eliminovat řadu běžných příčin chyb měření.Např. dotek by se měl povrchu výrobku dotýkat kolmo, kdykoli je to možné. Dotykové spínací sondy používané u souřadnicových měřicích strojů jsou navrženy tak, aby poskytovaly optimální výsledky, když se kulička doteku dotýká výrobku kolmo na povrch výrobku. V ideálním případě byste měli měřit při sklonu v rozmezí ±20° od kolmice, aby nedošlo ke sklouznutí kuličky doteku. Sklouznutí produkuje nekonzistentní, neopakovatelné výsledky.
Měření povrchu sondy
Přiblížení sondy musí být v rozmezí ±20° od kolmice, aby se minimalizovala chyba způsobená sklouznutím.

Vektory přiblížení sondy jsou kolmé na povrch koule.
Měření provedená paralelně k tělu sondy, tj. podél osy doteku, nejsou tak opakovatelná, jako měření provedená kolmo k ose.

Použití účinných metod dotekového měření
Měření sondou, která nejsou ani kolmá, ani paralelní k tělesu sondy (obr. 19), produkují výsledky, které jsou dokonce ještě méně opakovatelné než u měření provedených paralelně k tělesu sondy. Neprovádějte měření sondou paralelně k doteku a se sklonem vůči tělesu sondy, protože produkují velké chyby.

Použití účinných metod dotekového měření
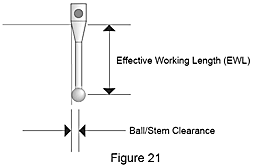
Pravděpodobnost doteku dříkem můžete snížit, použijete-li kuličku s velkým průměrem, čímž zvětšíte vzdálenost mezi dříkem a povrchem výrobku. Obecně platí, že čím větší je průměr kuličky, tím hlouběji se dotek dostane předtím, než se dotkne výrobku. Tomu se říká efektivní pracovní délka doteku (obr. 21). Rovněž, čím větší je kulička, tím na ní má menší dopad povrchová úprava výrobku, protože kontaktní bod je rozprostřený po větší ploše měřeného prvku. Nicméně největší průměr kuličky, jaký můžeme použít, je omezený průměrem nejmenších měřených otvorů.

Geometrické kótování a tolerance
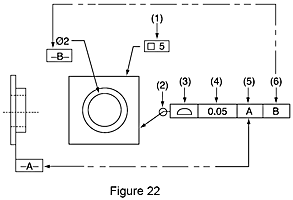
Geometrické kótování a tolerance (GD&T) je univerzální jazyk symbolů, hodně podobný mezinárodnímu systému dopravních značek, které radí řidičům, jak se mají pohybovat po silnicích. Symboly GD&T umožňují konstruktérům přesně a logicky popsat prvky dílu způsobem, který lze přesně vyrobit a zkontrolovat. GD&T se vyjadřuje v tolerančním rámci. Toleranční rámec prvku je jako základní věta, kterou je možné číst zleva doprava. Například toleranční rámec prvku na obrázku se čte následovně: 5mm čtvercový tvar (1) je řízen celkovou (2) tolerancí profilu (3) 0,05 mm (4), ve vztahu k primární základně A (5) a sekundární základně B (6). Tvar a tolerance určují limity variability výroby.

Tyto geometrické symboly se podobají symbolům používaným v mapách k označení prvků, např. dvouproudových a čtyřproudových dálnic, mostů a letišť. Podobají se novým mezinárodním dopravním značkám, které jsou častěji vidět na amerických dálnicích. Účelem těchto symbolů je také vytvořit společný jazyk, kterému bude každý rozumět.
Symboly geometrických charakteristik
Přímost – Stav, kdy jsou všechny body v přímce a tolerance je specifikována zónou tvořenou dvěma rovnoběžnými přímkami.
Rovinnost – Všechny body na povrchu jsou v jedné rovině a tolerance je specifikována zónou tvořenou dvěma paralelními rovinami.
Kruhovitost – Všechny body na povrchu jsou v kružnici. Tolerance je specifikována zónou ohraničenou dvěma soustřednými kružnicemi.
Válcovitost – Všechny body na otáčivém povrchu mají stejnou vzdálenost od společné osy. Tolerance válcovitosti specifikuje zónu tolerance ohraničenou dvěma soustřednými válci, uvnitř nichž musí povrch ležet.
Profil – Metoda tolerance pro kontrolu nepravidelných povrchů, čar, oblouků nebo normálních rovin. Profily je možné použít na jednotlivé čárové prvky nebo celý povrch dílu. Tolerance profilu specifikuje jednotnou hranici podél skutečného profilu, uvnitř níž musí ležet prvky povrchu.
Sklon – Stav povrchu nebo osy ve specifikovaném úhlu (jiném než 90°) od roviny nebo osy základny. Zóna tolerance je definována dvěma paralelními rovinami ve specifikovaném základním úhlu od roviny nebo osy základny.
Kolmost – Stav povrchu nebo osy v pravém úhlu od roviny nebo osy základny. Tolerance kolmosti specifikuje jednu z následujících možností: zónu definovanou dvěma rovinami kolmými k rovině nebo ose základny, nebo zónu definovanou dvěma paralelními rovinami kolmými k ose základny.
Rovnoběžnost – Stav povrchu nebo osy se stejnou vzdáleností všech bodů od roviny nebo osy základny. Tolerance rovnoběžnosti specifikuje jednu z následujících možností: zónu definovanou dvěma rovinami nebo čárami paralelními k rovině nebo ose základny, nebo zónu tolerance válcovitosti, jejíž osa je paralelní k ose základny.
Soustřednost – Osy všech průřezových prvků otáčivého povrchu jsou společné s osou prvku základny. Tolerance soustřednosti specifikuje zónu tolerance válcovitosti, jejíž osa se shoduje s osou základny.
Pozice – Tolerance pozice definuje zónu, ve které se může střední osa nebo střední rovina odchýlit od skutečné (teoreticky přesné) pozice. Základní rozměry určují skutečnou pozici od prvků údaje a mezi vzájemně spojenými prvky. Tolerance pozice je celková povolená odchylka polohy prvku od jeho přesného místa. U válcovitých prvků, jako jsou otvory nebo vnější průměry, je tolerance pozice obecně průměr zóny tolerance, ve které musí ležet osa prvku. U prvků, které nejsou kulaté, jako drážky, je tolerance pozice celková šířka zóny tolerance, ve které musí ležet středová rovina.
Kruhové házení – Umožňuje kontrolu kruhových prvků povrchu. Tolerance je nezávisle použita u každé kruhové měřicí pozice, když se díl otáčí o 360 stupňů. Tolerance kruhového házení použitá na povrchy konstruované kolem osy základny řídí kumulativní odchylky kruhovitosti a souososti. Při použití na povrchy konstruované vůči ose základny v pravých úhlech řídí kruhové prvky roviny.
Celkové házení — Poskytuje kombinovanou kontrolu všech prvků povrchu. Tolerance je použita současně na kruhové a podélné prvky, když se díl otáčí o 360 stupňů. Celkové házení řídí kumulativní odchylky kruhovitosti, válcovitosti, přímosti, souososti, hranatosti, sbíhavosti a profilu, když se použijí na povrchy konstruované kolem osy základny. Při použití na povrchy konstruované vůči ose základny v pravých úhlech řídí kumulativní odchylky kolmosti a rovinnosti.
Rovinnost – Všechny body na povrchu jsou v jedné rovině a tolerance je specifikována zónou tvořenou dvěma paralelními rovinami.
Kruhovitost – Všechny body na povrchu jsou v kružnici. Tolerance je specifikována zónou ohraničenou dvěma soustřednými kružnicemi.
Válcovitost – Všechny body na otáčivém povrchu mají stejnou vzdálenost od společné osy. Tolerance válcovitosti specifikuje zónu tolerance ohraničenou dvěma soustřednými válci, uvnitř nichž musí povrch ležet.
Profil – Metoda tolerance pro kontrolu nepravidelných povrchů, čar, oblouků nebo normálních rovin. Profily je možné použít na jednotlivé čárové prvky nebo celý povrch dílu. Tolerance profilu specifikuje jednotnou hranici podél skutečného profilu, uvnitř níž musí ležet prvky povrchu.
Sklon – Stav povrchu nebo osy ve specifikovaném úhlu (jiném než 90°) od roviny nebo osy základny. Zóna tolerance je definována dvěma paralelními rovinami ve specifikovaném základním úhlu od roviny nebo osy základny.
Kolmost – Stav povrchu nebo osy v pravém úhlu od roviny nebo osy základny. Tolerance kolmosti specifikuje jednu z následujících možností: zónu definovanou dvěma rovinami kolmými k rovině nebo ose základny, nebo zónu definovanou dvěma paralelními rovinami kolmými k ose základny.
Rovnoběžnost – Stav povrchu nebo osy se stejnou vzdáleností všech bodů od roviny nebo osy základny. Tolerance rovnoběžnosti specifikuje jednu z následujících možností: zónu definovanou dvěma rovinami nebo čárami paralelními k rovině nebo ose základny, nebo zónu tolerance válcovitosti, jejíž osa je paralelní k ose základny.
Soustřednost – Osy všech průřezových prvků otáčivého povrchu jsou společné s osou prvku základny. Tolerance soustřednosti specifikuje zónu tolerance válcovitosti, jejíž osa se shoduje s osou základny.
Pozice – Tolerance pozice definuje zónu, ve které se může střední osa nebo střední rovina odchýlit od skutečné (teoreticky přesné) pozice. Základní rozměry určují skutečnou pozici od prvků údaje a mezi vzájemně spojenými prvky. Tolerance pozice je celková povolená odchylka polohy prvku od jeho přesného místa. U válcovitých prvků, jako jsou otvory nebo vnější průměry, je tolerance pozice obecně průměr zóny tolerance, ve které musí ležet osa prvku. U prvků, které nejsou kulaté, jako drážky, je tolerance pozice celková šířka zóny tolerance, ve které musí ležet středová rovina.
Kruhové házení – Umožňuje kontrolu kruhových prvků povrchu. Tolerance je nezávisle použita u každé kruhové měřicí pozice, když se díl otáčí o 360 stupňů. Tolerance kruhového házení použitá na povrchy konstruované kolem osy základny řídí kumulativní odchylky kruhovitosti a souososti. Při použití na povrchy konstruované vůči ose základny v pravých úhlech řídí kruhové prvky roviny.
Celkové házení — Poskytuje kombinovanou kontrolu všech prvků povrchu. Tolerance je použita současně na kruhové a podélné prvky, když se díl otáčí o 360 stupňů. Celkové házení řídí kumulativní odchylky kruhovitosti, válcovitosti, přímosti, souososti, hranatosti, sbíhavosti a profilu, když se použijí na povrchy konstruované kolem osy základny. Při použití na povrchy konstruované vůči ose základny v pravých úhlech řídí kumulativní odchylky kolmosti a rovinnosti.
