Introduzione alla metrologia a coordinate
Conoscere la CMM: il sistema a coordinate.
Contattateci
Noi usiamo un sistema a coordinate per descrivere i movimenti di una macchina di misura. Il sistema a coordinate, inventato dal famoso filosofo e matematico francese René Descartes all’inizio del 1600, ci permette di localizzare gli elementi sui pezzi da misurare rispetto ad altri elementi.
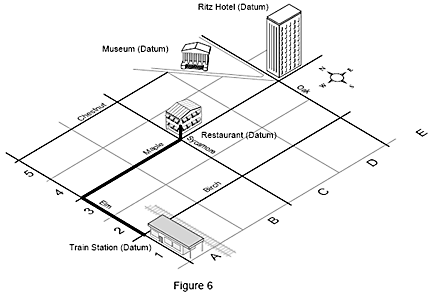
Il sistema a coordinate assomiglia molto a una carta topografica in cui la combinazione di una lettera lungo un bordo della carta, un numero lungo l’altro bordo e le altezze descrive ciascuna posizione sulla carta stessa. Questa combinazione di lettera, numero e altezza viene chiamata coordinata e rappresenta un punto specifico rispetto a tutti gli altri.
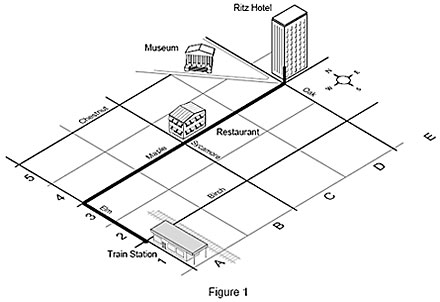
Un altro esempio è la cartina stradale che mostra gli edifici. Per arrivare alla vostra camera all’Hotel Ritz dalla stazione ferroviaria (vostro punto di partenza), camminate per 2 caseggiati lungo la Elm Street, 4 caseggiati sulla Maple e salite 3 piani al Ritz. Questa posizione può essere anche descritta dalle coordinate 4-E-3 sulla carta, che corrisponde agli assi X, Y e Z sulla macchina. Queste coordinate indicano in modo univoco la vostra camera e nessun’altra posizione sulla cartina.
Una macchina di misura a coordinate (CMM) è un po' come il dito che traccia le coordinate su di una cartina. I suoi tre assi formano il sistema di coordinate della macchina. Invece del dito, la CMM usa un sensore per misurare i punti su di un pezzo. Ogni punto sul pezzo è unico nel sistema di coordinate. La CMM unisce i punti misurati per formare un elemento che ora può essere messo in relazione con tutti gli altri elementi.
Prima dell’introduzione del software nella misura a coordinate, i pezzi venivano allineati fisicamente in modo parallelo agli assi della macchina in modo che i sistemi macchina e pezzo fossero paralleli tra loro. Questo richiedeva molto tempo e non era molto preciso. Se il pezzo era rotondo o sculturato piuttosto che quadrato o rettangolare, l’operazione di misura era quasi impossibile.
L'operazione di messa in relazione dei due sistemi di coordinate si chiama allineamento. Con la cartina stradale lo facciamo automaticamente girando la cartina in modo che sia parallela alla strada (riferimento) o a un punto cardinale (cioè nord). Quando facciamo questo, stiamo allineandoci al “sistema di coordinate mondo.”
Il sistema a coordinate assomiglia molto a una carta topografica in cui la combinazione di una lettera lungo un bordo della carta, un numero lungo l’altro bordo e le altezze descrive ciascuna posizione sulla carta stessa. Questa combinazione di lettera, numero e altezza viene chiamata coordinata e rappresenta un punto specifico rispetto a tutti gli altri.
Un altro esempio è la cartina stradale che mostra gli edifici. Per arrivare alla vostra camera all’Hotel Ritz dalla stazione ferroviaria (vostro punto di partenza), camminate per 2 caseggiati lungo la Elm Street, 4 caseggiati sulla Maple e salite 3 piani al Ritz. Questa posizione può essere anche descritta dalle coordinate 4-E-3 sulla carta, che corrisponde agli assi X, Y e Z sulla macchina. Queste coordinate indicano in modo univoco la vostra camera e nessun’altra posizione sulla cartina.


Una macchina di misura a coordinate (CMM) è un po' come il dito che traccia le coordinate su di una cartina. I suoi tre assi formano il sistema di coordinate della macchina. Invece del dito, la CMM usa un sensore per misurare i punti su di un pezzo. Ogni punto sul pezzo è unico nel sistema di coordinate. La CMM unisce i punti misurati per formare un elemento che ora può essere messo in relazione con tutti gli altri elementi.
Il sistema di coordinate: il sistema di coordinate macchina
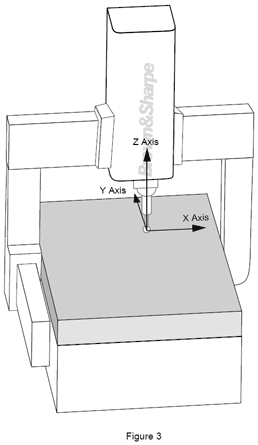
Vi sono due tipi di sistemi di coordinate nel mondo della misura. Il primo si chiama sistema di coordinate macchina. Qui gli assi X, Y, Z si riferiscono ai movimenti della macchina. Visto dalla parte anteriore della macchina, l’asse X va da sinistra a destra, l’asse Y va dal fronte al retro e l’asse Z va in alto e in basso, perpendicolare agli altri due.
Il sistema di coordinate: il sistema di coordinate pezzo
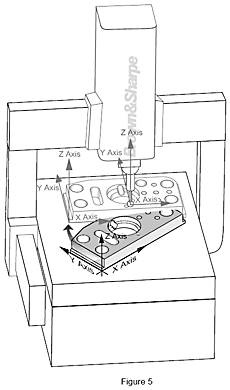
Il secondo sistema di coordinate è il sistema di coordinate pezzo in cui i tre assi si correlano ai riferimenti o elementi del pezzo da misurare.Prima dell’introduzione del software nella misura a coordinate, i pezzi venivano allineati fisicamente in modo parallelo agli assi della macchina in modo che i sistemi macchina e pezzo fossero paralleli tra loro. Questo richiedeva molto tempo e non era molto preciso. Se il pezzo era rotondo o sculturato piuttosto che quadrato o rettangolare, l’operazione di misura era quasi impossibile.
Il sistema di coordinate: che cos’è l’allineamento?
Con l'attuale software della CMM, la CMM misura i riferimenti del pezzo (dal disegno del pezzo), definisce il sistema di coordinate del pezzo e lo mette in relazione matematicamente con il sistema di coordinate macchina.L'operazione di messa in relazione dei due sistemi di coordinate si chiama allineamento. Con la cartina stradale lo facciamo automaticamente girando la cartina in modo che sia parallela alla strada (riferimento) o a un punto cardinale (cioè nord). Quando facciamo questo, stiamo allineandoci al “sistema di coordinate mondo.”

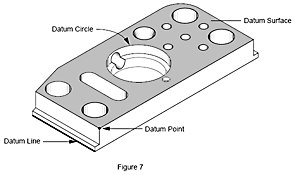
Che cos’è un riferimento?
Un riferimento è una posizione. Noi usiamo i riferimenti come guide per dire agli altri dove siamo o come direzioni per spiegare come arrivare in un luogo. Sulla cartina il Ritz Hotel è un riferimento. Lo sono anche le strade, la stazione ferroviaria, il museo e il ristorante. Usando un’origine, i riferimenti, le direzioni e le distanze, abbiamo quindi tutte le informazioni che ci servono per andare da un posto all’altro.
Ad esempio, per andare dalla stazione ferroviaria (origine) al ristorante, camminate per 2 caseggiati verso nord sulla Elm Street (riferimento), prendete a destra e camminate per 2 caseggiati verso est sulla Maple (riferimento).

In metrologia un riferimento è un elemento su di un pezzo come un foro, una superficie o un’asola. Noi misuriamo un pezzo per determinare la distanza tra un elemento e un altro.
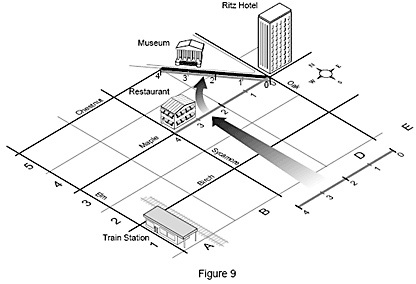
Tornando alla nostra cartina stradale, quando arrivate al vostro hotel e decidete di mangiare in un famoso ristorante durante la vostra visita in città, dovete trovarlo sulla cartina. L’hotel diventa ora il vostro nuovo punto di partenza od origine. Conoscendo la vostra posizione, se guardate la cartina vedrete che è necessario spostarsi di due caseggiati verso ovest lungo la Maple Street per raggiungere il ristorante.
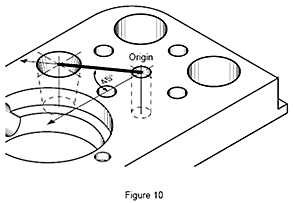
La stessa procedura si applica al pezzo (Figura 10). La distanza tra i due fori sul pezzo può essere misurata quando l’origine iniziale è stata traslata sul foro più piccolo e il sistema di coordinate pezzo è stato ruotato matematicamente di 45°. Ora entrambi i fori si trovano lungo il nuovo asse Y e la distanza può essere calcolata automaticamente.
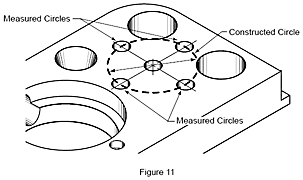
Altri elementi, come la distanza, la simmetria, l’intersezione, l’angolo e la proiezione, non possono essere misurati direttamente ma devono essere costruiti matematicamente partendo da elementi misurati prima che si possano determinare i loro valori. Questi vengono chiamati elementi costruiti. Nella Figura 11 il cerchio mediano viene costruito partendo dai punti centrali dei quattro cerchi misurati.
Le macchine di misura a coordinate non sono diverse da altri prodotti da questo punto di vista. Sono costruite con tolleranze estremamente strette ma nella loro struttura vi sono errori (roll, pitch, yaw, linearità, quadratura, errori di scala) che incidono sulla loro precisione. Poichè le tolleranze di produzione diventano sempre più strette, è necessario che le CMM diventino più precise.
La maggior parte delle imprecisioni della CMM può essere corretta automaticamente dal computer della CMM. Misurati tutti gli errori geometrici della CMM (la mappatura degli errori), questi possono essere ridotti al minimo o addirittura eliminati con i potenti algoritmi del software della CMM. Questa tecnica viene chiamata compensazione volumetrica degli errori.
Eliminando gli errori matematicamente si abbassa il costo di produzione e si incrementa il rendimento dell'investimento del cliente.
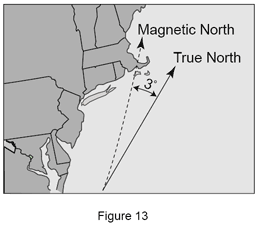
È più facile comprendere la compensazione volumetrica se consideriamo il rapporto esistente tra una cartina e una bussola. Se volete navigare verso un determinato luogo, dovete conoscere la vera direzione rispetto alla vostra attuale posizione (origine). Per determinare la direzione o traiettoria si usano una bussola e una carta. C’è tuttavia una differenza tra nord vero e nord magnetico. La differenza tra i due viene chiamata variazione ed è causata dalla non uniformità nel campo magnetico della terra. Pertanto per determinare la vera direzione da un punto a un altro, è necessario aggiungere o sottrarre la variazione tra vero nord e nord magnetico dalla traiettoria della bussola.
Nella carta qui di seguito, la differenza tra il vero nord e il nord magnetico (3° O) dev'essere compensata altrimenti un marinaio finirebbe a nord-ovest della destinazione voluta e si arenerebbe prima della destinazione finale.
La macchina di misura esegue automaticamente una compensazione simile per eliminare le variazioni della macchina dalla misura.
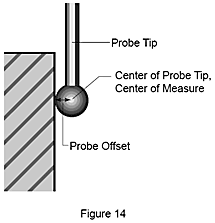
Noti il centro e il raggio della punta, quando il tastatore va a contatto del pezzo, le coordinate della punta sono matematicamente "compensate" dal raggio della punta al punto di contatto effettivo della punta (Figura 14). La direzione dell'offset viene determinata automaticamente dalla procedura di allineamento.
Facciamo un'operazione simile quando parcheggiamo l'auto. Meglio riusciamo a valutare il nostro offset dall'esterno dell'auto e più vicini riusciamo a parcheggiare al bordo del marciapiede.
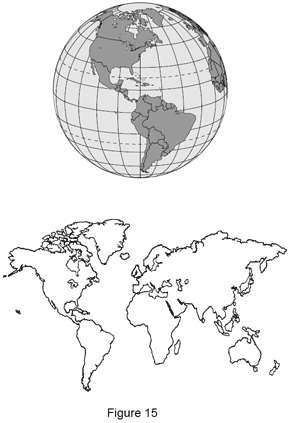
La proiezione di un elemento del pezzo su di un altro può essere paragonata alla creazione della carta geografica "piatta" tradizionale del mondo (proiezione di Mercatore). La mappa in piano viene creata proiettando il globo terrestre (sfera) su di un cilindro.
In metrologia le proiezioni vi permettono di misurare in modo più preciso come i componenti si accoppieranno nell'assemblaggio finale. Nella misura dei cilindri dell'industria automobilistica (ad esempio i monoblocchi), proiettando un cilindro sul piano della testata, si può determinare con precisione come si accoppieranno i pistoni nel cilindro e il comportamento della camera di combustione nella testata.
Sono necessari almeno tre punti per misurare il diametro di un cerchio e se quei punti non sono alla stessa distanza dalla parte superiore del foro, il diametro misurato apparirà ellittico. Per superare il problema di questa errata rappresentazione, i dati di misura vengono proiettati su di un piano perpendicolare alla linea media del cilindro. Il risultato è la determinazione precisa della vera dimensione dell'elemento di questo componente.
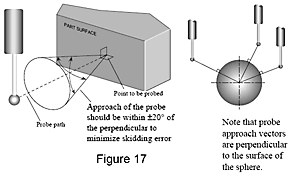
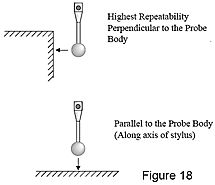
Le misure del tastatore, ad esempio, devono essere eseguite perpendicolarmente alla superficie del pezzo ogni qual volta è possibile. I tastatori punto a punto usati sulle macchine di misura a coordinate sono progettati per fornire risultati ottimali quando la punta del tastatore tocca il pezzo perpendicolarmente al corpo del tastatore. In una situazione ideale, si dovrebbero prendere punti entro ±20° dalla perpendicolare per evitare che la punta del tastatore slitti. Lo slittamento produce risultati non coerenti e non ripetibili.
I rilevamenti effettuati parallelamente al corpo del tastatore, cioè lungo l'asse dello stilo, non sono ripetibili come quelli effettuati perpendicolarmente all'asse.
Il tallonamento è un'altra causa di errore di misura (Figura 20). Quando il tastatore tocca il pezzo con lo stelo anziché con la punta dello stilo, il sistema di misura presume che il rilevamento sia stato eseguito in modo normale e si verificheranno errori importanti.
I punti di misura rilevati con tastatore elettronico vengono registrati quando lo stilo viene deflesso al punto da aprire meccanicamente i contatti elettrici o generare forza sufficiente ad attivare i circuiti sensibili alla pressione. La disposizione fisica dei contatti causa dei leggeri errori nella precisione anche se questi verranno ridotti nella qualifica del tastatore. Tuttavia più lunga è la prolunga della punta del tastatore, maggiore è l'errore di pre-corsa e maggiore l'errore residuo dopo la qualifica del tastatore. I tastatori più lunghi non sono rigidi come quelli più corti. Maggiore la deflessione dello stilo, minore la precisione. Si dovrebbe evitare l'uso di tastatori che abbiano stili e prolunghe molto lunghi.
Vi sono sette forme, chiamate elementi geometrici, usate per definire un pezzo e i suoi elementi. Le forme sono: punto, linea, piano, cerchio, cilindro, cono e sfera. Vi sono anche alcune caratteristiche geometriche che determinano la condizione dei pezzi e la relazione tra gli elementi.
Questi simboli geometrici sono simili ai simboli usati sulle carte geografiche per indicare elementi come autostrade a due o quattro corsie, ponti e aeroporti. Sono come i nuovi segnali stradali internazionali che si vedono di frequente sulle autostrade statunitensi. Lo scopo di questi simboli è quello di formare una lingua comune che tutti possano capire.
Ad esempio, per andare dalla stazione ferroviaria (origine) al ristorante, camminate per 2 caseggiati verso nord sulla Elm Street (riferimento), prendete a destra e camminate per 2 caseggiati verso est sulla Maple (riferimento).

In metrologia un riferimento è un elemento su di un pezzo come un foro, una superficie o un’asola. Noi misuriamo un pezzo per determinare la distanza tra un elemento e un altro.

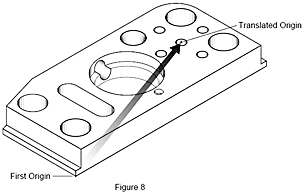
Che cos’è la traslazione?
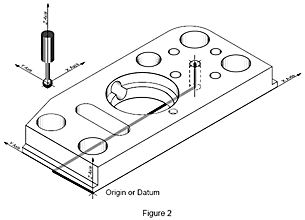
Ipotizziamo di voler conoscere la distanza tra un elemento specifico di un pezzo e un altro elemento. Si prenda ad esempio la distanza dei centri di ciascuno dei quattro fori da un foro centrale. Per fare questo, dapprima si misura il foro centrale, si trasla l’origine al centro di questo foro e poi si misura ciascuno dei quattro fori attorno. Lo spostamento del punto di partenza (origine) della misura dalla sua posizione attuale a un altro punto sul pezzo si chiama traslazione. La CMM lo fa automaticamente quando si chiede una procedura di allineamento al software di misura geometrico.Tornando alla nostra cartina stradale, quando arrivate al vostro hotel e decidete di mangiare in un famoso ristorante durante la vostra visita in città, dovete trovarlo sulla cartina. L’hotel diventa ora il vostro nuovo punto di partenza od origine. Conoscendo la vostra posizione, se guardate la cartina vedrete che è necessario spostarsi di due caseggiati verso ovest lungo la Maple Street per raggiungere il ristorante.

Che cos’è la rotazione?
Non tutti i riferimenti sono perpendicolari rispetto ad altri riferimenti. Ad esempio, se guardate la vostra cartina stradale vedrete che il museo si trova su di una strada che non è né parallela né perpendicolare alle strade in cui si trovano hotel, ristorante e stazione ferroviaria. Di conseguenza, per stabilire la distanza dall’hotel al museo, prima dovete traslare la vostra origine all’hotel e poi ruotarla perché sia parallela alla strada in cui si trova il museo. Ora potete facilmente misurare la distanza dal museo all’hotel.
La stessa procedura si applica al pezzo (Figura 10). La distanza tra i due fori sul pezzo può essere misurata quando l’origine iniziale è stata traslata sul foro più piccolo e il sistema di coordinate pezzo è stato ruotato matematicamente di 45°. Ora entrambi i fori si trovano lungo il nuovo asse Y e la distanza può essere calcolata automaticamente.

Elementi misurati e costruiti
Qual è la differenza tra elementi misurati e costruiti? La grande maggioranza dei pezzi è costituita di semplici elementi geometrici creati con la lavorazione o la formatura. Questi elementi primari (piani, bordi, cilindri, sfere, coni, ecc.) vengono chiamati elementi. Quando una CMM può misurare questi elementi direttamente toccando le superfici che costituiscono l’elemento con un tastatore, gli elementi vengono chiamati elementi misurati.Altri elementi, come la distanza, la simmetria, l’intersezione, l’angolo e la proiezione, non possono essere misurati direttamente ma devono essere costruiti matematicamente partendo da elementi misurati prima che si possano determinare i loro valori. Questi vengono chiamati elementi costruiti. Nella Figura 11 il cerchio mediano viene costruito partendo dai punti centrali dei quattro cerchi misurati.

Elementi costruiti
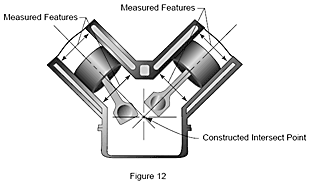
Le relazioni tra un elemento o gruppo di elementi rispetto a un altro elemento o gruppo di elementi sono essenziali per la produzione. Ad esempio, il punto di intersezione tra i cilindri su di un lato del blocco motore e quelli sull’altro lato determina la bontà dell’accoppiamento dei pezzi. Questo punto di intersezione è costruito partendo dai due elementi misurati (i cilindri motore).
Che cos’è la compensazione volumetrica?
Anche se la tecnologia di produzione avanzata rende possibile applicare tolleranze e fabbricare i pezzi in modo molto preciso, le imperfezioni esistono ancora. Per quanto ridotte, il fatto che ci siano tolleranze significa che vi sono errori.Le macchine di misura a coordinate non sono diverse da altri prodotti da questo punto di vista. Sono costruite con tolleranze estremamente strette ma nella loro struttura vi sono errori (roll, pitch, yaw, linearità, quadratura, errori di scala) che incidono sulla loro precisione. Poichè le tolleranze di produzione diventano sempre più strette, è necessario che le CMM diventino più precise.
La maggior parte delle imprecisioni della CMM può essere corretta automaticamente dal computer della CMM. Misurati tutti gli errori geometrici della CMM (la mappatura degli errori), questi possono essere ridotti al minimo o addirittura eliminati con i potenti algoritmi del software della CMM. Questa tecnica viene chiamata compensazione volumetrica degli errori.
Eliminando gli errori matematicamente si abbassa il costo di produzione e si incrementa il rendimento dell'investimento del cliente.
È più facile comprendere la compensazione volumetrica se consideriamo il rapporto esistente tra una cartina e una bussola. Se volete navigare verso un determinato luogo, dovete conoscere la vera direzione rispetto alla vostra attuale posizione (origine). Per determinare la direzione o traiettoria si usano una bussola e una carta. C’è tuttavia una differenza tra nord vero e nord magnetico. La differenza tra i due viene chiamata variazione ed è causata dalla non uniformità nel campo magnetico della terra. Pertanto per determinare la vera direzione da un punto a un altro, è necessario aggiungere o sottrarre la variazione tra vero nord e nord magnetico dalla traiettoria della bussola.
Nella carta qui di seguito, la differenza tra il vero nord e il nord magnetico (3° O) dev'essere compensata altrimenti un marinaio finirebbe a nord-ovest della destinazione voluta e si arenerebbe prima della destinazione finale.
La macchina di misura esegue automaticamente una compensazione simile per eliminare le variazioni della macchina dalla misura.

Qualifica della punta del tastatore
In generale le CMM rilevano i dati toccando il pezzo con un tastatore (un tastatore rigido o un tastatore elettronico punto a punto) montato sull'asse di misura della macchina. Anche se la punta del tastatore è molto precisa, quando il tastatore è fissato alla CMM, la posizione della punta nel sistema di riferimento macchina dev'essere determinato prima della misura. Poiché è la circonferenza della punta a toccare il pezzo, il centro e il raggio del tastatore sono determinati misurando una sfera molto precisa (sfera di qualifica).Noti il centro e il raggio della punta, quando il tastatore va a contatto del pezzo, le coordinate della punta sono matematicamente "compensate" dal raggio della punta al punto di contatto effettivo della punta (Figura 14). La direzione dell'offset viene determinata automaticamente dalla procedura di allineamento.
Facciamo un'operazione simile quando parcheggiamo l'auto. Meglio riusciamo a valutare il nostro offset dall'esterno dell'auto e più vicini riusciamo a parcheggiare al bordo del marciapiede.

Proiezioni
Una proiezione è la riproduzione di un elemento del pezzo su di un altro elemento come la proiezione di un cerchio o una linea su di un piano o un punto su di una linea.La proiezione di un elemento del pezzo su di un altro può essere paragonata alla creazione della carta geografica "piatta" tradizionale del mondo (proiezione di Mercatore). La mappa in piano viene creata proiettando il globo terrestre (sfera) su di un cilindro.

In metrologia le proiezioni vi permettono di misurare in modo più preciso come i componenti si accoppieranno nell'assemblaggio finale. Nella misura dei cilindri dell'industria automobilistica (ad esempio i monoblocchi), proiettando un cilindro sul piano della testata, si può determinare con precisione come si accoppieranno i pistoni nel cilindro e il comportamento della camera di combustione nella testata.
Sono necessari almeno tre punti per misurare il diametro di un cerchio e se quei punti non sono alla stessa distanza dalla parte superiore del foro, il diametro misurato apparirà ellittico. Per superare il problema di questa errata rappresentazione, i dati di misura vengono proiettati su di un piano perpendicolare alla linea media del cilindro. Il risultato è la determinazione precisa della vera dimensione dell'elemento di questo componente.

Impiego di metodi di rilevamento efficaci
Con l'impiego di metodi efficaci quando si verifica un pezzo, si possono eliminare molte cause comuni di errore di misura.Le misure del tastatore, ad esempio, devono essere eseguite perpendicolarmente alla superficie del pezzo ogni qual volta è possibile. I tastatori punto a punto usati sulle macchine di misura a coordinate sono progettati per fornire risultati ottimali quando la punta del tastatore tocca il pezzo perpendicolarmente al corpo del tastatore. In una situazione ideale, si dovrebbero prendere punti entro ±20° dalla perpendicolare per evitare che la punta del tastatore slitti. Lo slittamento produce risultati non coerenti e non ripetibili.
Superficie del pezzo da rilevare
L'approccio del tastatore dev'essere entro ±20° della perpendicolare per minimizzare l'errore di slittamento. I vettori di approccio del tastatore sono perpendicolari alla superficie della sfera.
I rilevamenti effettuati parallelamente al corpo del tastatore, cioè lungo l'asse dello stilo, non sono ripetibili come quelli effettuati perpendicolarmente all'asse.

Impiego di metodi di rilevamento efficaci
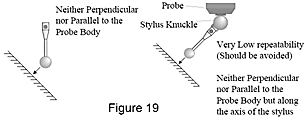
I rilevamenti che non sono né perpendicolari né paralleli al corpo del tastatore (Figura 19) producono risultati che sono persino meno ripetibli di quelli paralleli al corpo del tastatore. Si deve evitare di eseguire rilevamenti paralleli allo stilo e perpendicolari rispetto al corpo del tastatore perché produrranno errori di grande entità.
Il tallonamento è un'altra causa di errore di misura (Figura 20). Quando il tastatore tocca il pezzo con lo stelo anziché con la punta dello stilo, il sistema di misura presume che il rilevamento sia stato eseguito in modo normale e si verificheranno errori importanti.
Impiego di metodi di rilevamento efficaci
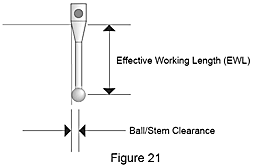
Si può ridurre la probabilità di tallonamento usando una punta di diametro maggiore per aumentare la distanza tra sfera/stelo e superficie del pezzo. In generale, maggiore è il diametro della punta e più in profondità potrà andare lo stilo prima di toccare l'elemento del pezzo. Questa viene chiamata la lunghezza di lavoro utile del tastatore (Figura 21). Inoltre, maggiore è il diametro della punta, minore effetto avrà sulla finitura superficiale del pezzo poiché il punto di contatto è diffuso su di un'area più ampia dell'elemento misurato. Ma la punta più grande possibile è limitata dalla dimensione dei fori da misurare più piccoli.
I punti di misura rilevati con tastatore elettronico vengono registrati quando lo stilo viene deflesso al punto da aprire meccanicamente i contatti elettrici o generare forza sufficiente ad attivare i circuiti sensibili alla pressione. La disposizione fisica dei contatti causa dei leggeri errori nella precisione anche se questi verranno ridotti nella qualifica del tastatore. Tuttavia più lunga è la prolunga della punta del tastatore, maggiore è l'errore di pre-corsa e maggiore l'errore residuo dopo la qualifica del tastatore. I tastatori più lunghi non sono rigidi come quelli più corti. Maggiore la deflessione dello stilo, minore la precisione. Si dovrebbe evitare l'uso di tastatori che abbiano stili e prolunghe molto lunghi.
Tolleranze geometriche
Le tolleranze geometriche (GD&T) sono un linguaggio universale fatto di simboli, molto simile al sistema internazionale di segnali stradali che informano chi guida. I simboli GD&T permettono ai progettisti di descrivere in modo logico e preciso gli elementi del pezzo in modo che possano essere fabbricati e verificati con precisione. Le tolleranze geometriche sono espresse nelle caselle di controllo (feature control frame). La casella di controllo è come una frase semplice che può essere letta da sinistra a destra. Ad esempio la casella di controllo illustrata qui significa: La forma quadrata di 5 mm (1) è controllata da una tolleranza di profilo (3) perimetrale (2) di 0,05 mm (4), in relazione al riferimento primario A (5) e al riferimento secondario B (6). La forma e la tolleranza determinano i limiti di variabilità della produzione.
Vi sono sette forme, chiamate elementi geometrici, usate per definire un pezzo e i suoi elementi. Le forme sono: punto, linea, piano, cerchio, cilindro, cono e sfera. Vi sono anche alcune caratteristiche geometriche che determinano la condizione dei pezzi e la relazione tra gli elementi.
Questi simboli geometrici sono simili ai simboli usati sulle carte geografiche per indicare elementi come autostrade a due o quattro corsie, ponti e aeroporti. Sono come i nuovi segnali stradali internazionali che si vedono di frequente sulle autostrade statunitensi. Lo scopo di questi simboli è quello di formare una lingua comune che tutti possano capire.
Simboli geometrici caratteristici
- Linearità - condizione in cui tutti i punti si trovano su di una linea retta, la tolleranza specificata da una zona formata da due linee parallele.
- Planarità - Tutti i punti su di una superficie sono in un piano, la tolleranza specificata da una zona formata da due piani paralleli.
- Circolarità - Tutti i punti su di una superficie sono in un cerchio. La tolleranza è specificata da una zona delimitata da due cerchi concentrici.
- Cilindricità - Tutti i punti di una superficie di rivoluzione sono equidistanti da un asse comune. La tolleranza di cilindricità specifica una zona di tolleranza delimitata da due cilindri concentrici entro i quali deve trovarsi la superficie.
- Profilo - Metodo di tolleranza che controlla superfici, linee, archi irregolari o piani normali. I profili possono essere applicati a singoli elementi linea o all'intera superficie di un pezzo. La tolleranza del profilo specifica un confine uniforme lungo il vero profilo entro il quale devono trovarsi gli elementi della superficie.
- Angolarità - La condizione di una superficie o asse a un angolo specificato (diverso da 90°) rispetto a un piano o asse di riferimento. La zona di tolleranza viene definita da due piani paralleli all'angolo di base specificato da un piano o asse di riferimento.
- Perpendicolarità - La condizione di una superficie o asse perpendicolare rispetto a un piano o asse di riferimento. La tolleranza di perpendicolarità specifica uno dei seguenti: una zona definita da due piani perpendicolari a un piano o asse di riferimento, o una zona definita da due piani paralleli perpendicolari all'asse di riferimento.
- Parallelismo - La condizione di una superficie o asse equidistante in tutti i punti da un piano o asse di riferimento. La tolleranza di parallelismo specifica uno dei seguenti: una zona definita da due piani o linee paralleli a un piano o asse di riferimento, o una zona di tolleranza cilindrica il cui asse sia parallelo a un asse di riferimento.
- Concentricità - Gli assi di tutti gli elementi a sezione trasversale di una superficie di rotazione sono comuni all'asse dell'elemento di riferimento. La tolleranza di concentricità specifica una zona di tolleranza cilindrica il cui asse coincide con l'asse di riferimento.
- Posizione - La tolleranza di posizione definisce una zona in cui l'asse centrale o il piano centrale può variare dalla posizione teoricamente esatta. Le dimensioni di base stabiliscono la posizione reale dagli elementi di riferimento e tra elementi correlati. La tolleranza di posizione è la variazione totale ammessa di posizione di un elemento rispetto alla sua posizione esatta. Per gli elementi cilindrici come i fori e i diametri esterni, la tolleranza di posizione è generalmente il diametro della zona di tolleranza nel quale deve trovarsi l'asse dell'elemento. Per elementi che non sono rotondi come le asole e i perni, la tolleranza di posizione è la larghezza totale della zona di tolleranza in cui deve trovarsi il piano centrale dell'elemento.
- Oscillazione circolare - Fornisce il controllo degli elementi circolari di una superficie. La tolleranza viene applicata indipendentemente a qualunque posizione di misura circolare ruotando il pezzo di 360 gradi. La tolleranza di circolarità applicata a superfici costruite attorno a un asse di riferimento controlla le variazioni cumulative di circolarità e coassialità. Quando viene applicata a superfici costruite perpendicolarmente all'asse di riferimento, controlla gli elementi circolari di un piano.
- Eccentricità totale - Fornisce il controllo composto di tutti gli elementi della superficie. La tolleranza applicata simultaneamente a elementi circolari e longitudinali ruotando il pezzo di 360 gradi. L'eccentricità totale controlla la variazione cumulativa di circolarità, cilindricità, linearità, coassialità, angolarità, conicità e profilo quando è applicata a superfici costruite attorno a un asse di riferimento. Quando è applicata a superfici costruite perpendicolarmente a un asse di riferimento, controlla variazioni cumulative di perpendicolarità e planarità.
