Einführung in die Koordinatenmesstechnik
Koordinatenmessgeräte verstehen: Das Koordinatensystem.
Kontakt
Wir nutzen ein Koordinatensystem um die Bewegungen eines Koordinatenmessgeräts zu beschreiben. Das, vom berühmten französischen Philosophen und Mathematiker René Descartes Anfang der 1600er Jahre, entwickelte Koordinatensystem, ermöglicht uns die Definition der Position von Elementen relativ zu anderen Elementen auf Werkstücken.
Ein Koordinatensystem ist vergleichbar mit einer Höhenkarte, auf der eine Kante mit Buchstaben und der anderen Kante mit Zahlen gekennzeichnet. Die Kombination aus Buchstabe und Zahl in Verbindung mit der angeführten Höhe beschreibt jeden Punkt auf der Karte unmissverständlich. Diese Kombination aus Buchstabe, Zahl und Höhe wird als Koordinate bezeichnet. Sie repräsentiert einen bestimmten Ort relativ zu allen anderen.
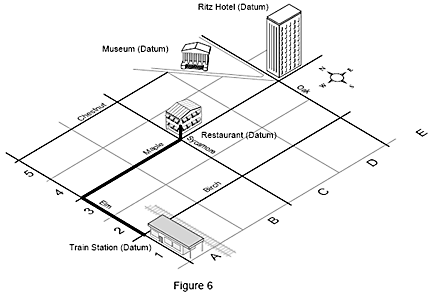
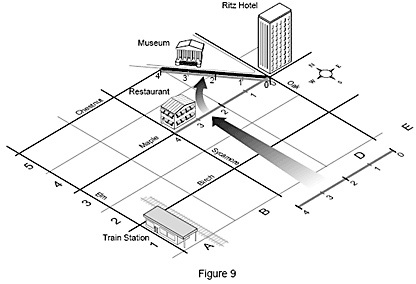
Ein anderes Beispiel ist eine Straßenkarte, die Gebäude enthält. Um vom Bahnhof, Ihrem Ausgangspunkt, zu Ihrem Zimmer im Hotel Ritz zu gelangen, gehen Sie zwei Blocks weit auf der Elm Street, dann vier Blocks entlang der Maple Street und im Hotel Ritz schließlich drei Stockwerke nach oben. Diese Position auf der Karte lässt sich auch durch die Koordinaten 4-E-3, die der X-, Y- und Z-Achse des Messgeräts entsprechen, beschreiben. Durch diese Koordinaten wird einzig und allein Ihr Hotelzimmer und kein anderer Ort auf der Karte definiert.
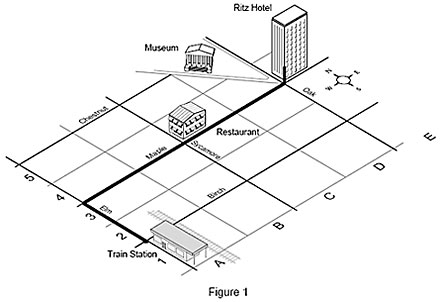
Ein Koordinatenmessgerät (KMG) arbeitet im Grunde genommen genau wie Ihr Finger, wenn Sie den Koordinaten auf der Karte folgen. Die drei Achsen des Koordinatenmessgeräts bilden dessen Koordinatensystem. Anstelle eines Fingers nutzt das KMG jedoch einen Sensor, um Punkte auf einem Werkstück zu messen. Jeder Punkt auf dem Werkstück existiert im Koordinatensystem des Messgeräts nur ein einziges Mal. Das KMG fügt die Messpunkte zusammen, um daraus ein Element zu bilden, das zu allen anderen Elementen in Beziehung gesetzt werden kann.
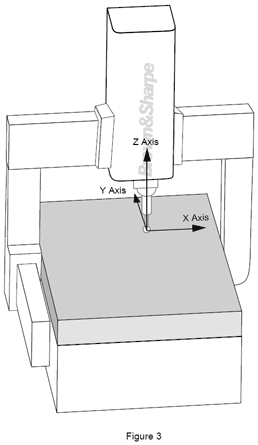
Das Koordinatensystem: Das Koordinatensystem des KMG
Das Koordinatensystem: Das Koordinatensystem des Werkstücks
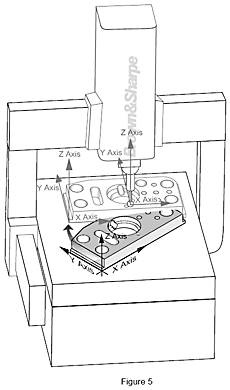
Das Koordinatensystem: Was versteht man unter Ausrichtung?
Mit moderner Messsoftware misst das KMG die Bezugselemente des Werkstücks (laut Konstruktionszeichnung), erstellt das Koordinatensystem des Werkstücks und setzt es mathematisch in Bezug zum Koordinatensystem des KMG.Der Prozess dieses Inbezugsetzens der beiden Koordinatensysteme wird als Ausrichtung bezeichnet. Bei einer Straßenkarte machen wir dies automatisch, indem wir die Karte so drehen, dass sie parallel zur Straße (Bezugselement) oder zu einer Himmelsrichtung (z. B. Norden) ausgerichtet ist. Dabei richten wir uns sozusagen am „Koordinatensystem der Welt“ aus.

Was ist ein Bezugselement?
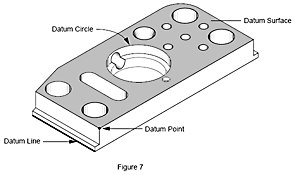
In der industriellen Messtechnik ist ein Bezugselement eine Eigenschaft eines Werkstücks, beispielsweise eine Bohrung, eine Oberfläche oder ein Langloch. Wir vermessen ein Werkstück, um den Abstand zwischen zwei Elementen zu ermitteln.
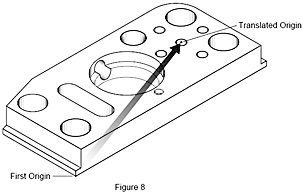
Was bedeutet Translation?
Was bedeutet Rotation?
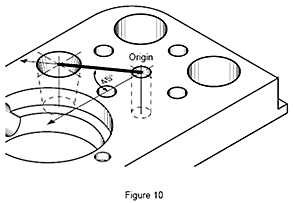
Gemessene und konstruierte Elemente
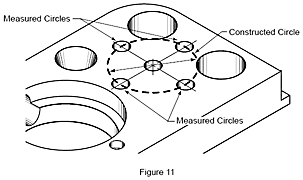
Konstruierte Elemente
Was bedeutet Volumenkompensation?
Koordinatenmessgeräte unterscheiden sich in dieser Hinsicht nicht von anderen Produkten. Obwohl bei ihrem Bau extrem enge Toleranzen eingehalten werden, weisen sie Fehler in ihrer Struktur auf (Roll-, Nick- und Gierwinkel, Geradheit, Rechtwinkligkeit und Skalenfehler), die sich auf ihre Genauigkeit auswirken. Da die Toleranzen in der Fertigung immer enger werden, müssen unsere KMG auch immer genauer werden.
Der Großteil der Ungenauigkeiten eines KMG kann von diesem automatisch rechnerisch kompensiert werden. Sobald alle geometrischen Fehler des KMG gemessen und in einer Fehlermatrix erfasst sind, können sie über leistungsfähige Algorithmen in der KMG-Software minimiert oder sogar vollständig beseitigt werden. Dieses Verfahren wird als volumetrische Fehlerkompensation bezeichnet.
Durch den mathematischen Ausgleich von Fehlern werden Fertigungskosten reduziert, und der Kunde profitiert von einer besseren Messleistung.
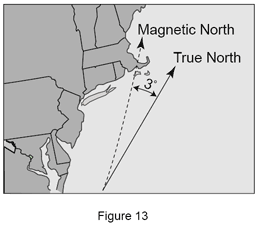
Wie die volumetrische Fehlerkompensation funktioniert, lässt sich anhand der Beziehung zwischen einer Karte und einem Kompass einfach illustrieren. Wenn Sie auf dem Meer zu einem bestimmten Punkt segeln wollen, dann müssen Sie – ausgehend von Ihrer aktuellen Position (Ihrem Nullpunkt) – wissen, in welcher wahren Richtung dieser Punkt liegt. Mithilfe eines Kompasses und einer Karte bestimmen Sie Ihre Richtung (Azimut). Allerdings unterscheidet sich die wahre Nordrichtung von der magnetischen Nordrichtung. Der Unterschied zwischen den beiden wird als Abweichung bezeichnet. Diese Abweichung wird durch die Schwankungen im Magnetfeld der Erde verursacht. Zur Ermittlung der wahren Richtung zwischen zwei Punkten muss die Abweichung zwischen der wahren und der magnetischen Nordrichtung in der Kompasspeilung durch Addition oder Subtraktion berücksichtigt werden.
In der dargestellten Karte muss der Unterschied zwischen der wahren und der magnetischen Nordrichtung (3° W) kompensiert werden, da das Segelboot andernfalls vom richtigen Kurs abkäme und in nordwestlicher Richtung auf Grund liefe, statt sein Ziel zu erreichen.
Eine ähnliche Kompensation führt ein KMG automatisch durch, um Abweichungen des Systems bei der Messung auszugleichen.
Kalibrierung von Tastspitzen
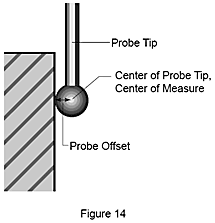
Sind der Mittelpunkt und der Radius der Tastspitze bekannt, werden die Koordinaten der Spitze mathematisch um den Radius (auch bezeichnet als Offset oder Versatz) bereinigt, um den tatsächlichen Berührungspunkt zu berechnen, sobald ein Werkstück angetastet wird (Abbildung 14). Die Richtung, in der dieser Versatz anzuwenden ist, wird beim Ausrichtvorgang automatisch ermittelt.
Beim Einparken eines Autos gehen wir ähnlich vor. Je besser wir in der Lage sind, den Abstand unseres Autos vom Randstein abzuschätzen, umso näher am Randstein können wir das Auto parken.
Projektionen
Die Projektion von einem Element auf ein anderes kann man sich vorstellen wie die Mercator-Projektion zur Erstellung einer Weltkarte. Die Weltkarte entsteht durch die Projektion der Weltkugel auf einen Zylinder.
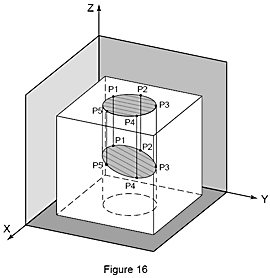
Um den Durchmesser eines Kreises zu messen, werden mindestens drei Punkte benötigt. Weisen nicht alle Punkte denselben Abstand von der Oberkante der Bohrung auf, ergibt sich eine Ellipse. Um diese falsche Darstellung auszugleichen, werden die Messdaten in eine Ebene projiziert, die rechtwinklig zur Mittelachse des Zylinders steht. So kann die tatsächliche Größe dieses Elements des Werkstücks genau bestimmt werden.
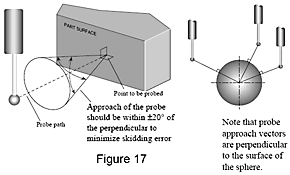
Durch die Anwendung effektiver Antastverfahren bei der Inspektion von Werkstücken können viele häufige Fehlerquellen von vornherein ausgeschaltet werden.
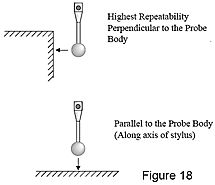
Beispielsweise sollten Messungen mit dem Taster nach Möglichkeit immer rechtwinklig zur Oberfläche des Werkstücks ausgeführt werden. Schaltende Taster sind so konzipiert, dass sie optimale Ergebnisse erzielen, wenn die Tastspitze das Werkstück im rechten Winkel zum Tasterkörper berührt. Im Idealfall sollten Messungen im Bereich von ±20° von der Senkrechten vorgenommen werden, um ein Abrutschen der Tastspitze zu vermeiden. Rutscht die Tastspitze, führt dies zu uneinheitlichen, nicht wiederholbaren Messergebnissen.
Zu messende Werkstückoberfläche
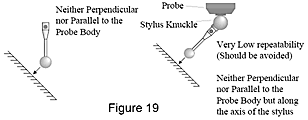
Antastpunkte, die weder rechtwinklig noch parallel zum Tasterkörper erfasst wurden (Abbildung 19), liefern Ergebnisse, die noch weniger gut wiederholbar sind als solche, die parallel zum Tasterkörper erfasst wurden. Vermeiden Sie die Erfassung von Antastpunkten parallel zum Taster und in einem Winkel zum Tasterkörper, da dadurch erhebliche Fehler entstehen können.
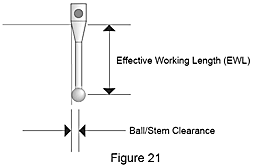
Die Wahrscheinlichkeit der Berührung des Werkstücks mit dem Schaft kann durch die Verwendung einer Tastspitze mit größerem Durchmesser zur Erhöhung des Sicherheitsabstands zwischen der Kugel bzw. dem Schaft und der Werkstückoberfläche reduziert werden. Generell gilt: Je größer der Durchmesser der Tastspitze, desto weiter nach unten kann sich der Taster bewegen, bevor er das Element auf dem Werkstück berührt. Dies wird als die effektive Arbeitslänge des Tasters (Abbildung 21) bezeichnet. Dazu kommt, dass die Oberflächenbeschaffenheit mit zunehmender Größe der Tastspitze an Bedeutung verliert, da der Kontaktpunkt mehr Raum auf dem Werkstück einnimmt. Die Größe der zu verwendenden Tastspitze wird jedoch durch die Größe der kleinsten zu messenden Bohrung begrenzt.
Form- und Lagetoleranzen
Form- und Lagetoleranzen (FLT) sind eine universelle Symbolsprache (ähnlich Verkehrsschildern) für die Eintragung von zulässigen Toleranzen in Zeichnungen. Anhand der Symbole für Form- und Lagetoleranzen können Konstrukteure die Elemente von Werkstücken präzise und logisch beschreiben, damit diese exakt gefertigt und geprüft werden können. Form- und Lagetoleranzen werden in einem Toleranzrahmen angeführt. Dieser Toleranzrahmen ist wie ein einfacher Satz von links nach rechts zu lesen. So bedeuten die Angaben im unten abgebildeten Toleranzrahmen beispielsweise Folgendes: Für die 5 Millimeter große quadratische Form (1) gilt rundherum (2) eine Profiltoleranz (3) von 0,05 Millimeter (4) in Bezug auf den Primärbezug A (5) und den Sekundärbezug B (6). Die Form und die Toleranz bestimmen die Grenzen der zulässigen Produktionsschwankungen.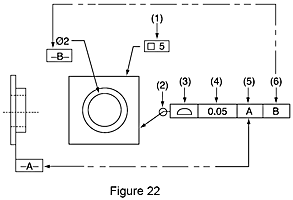
Die Symbole für die geometrischen Eigenschaften ähneln jenen auf Landkarten, die beispielsweise für Arten von Straßen, Brücken oder Flughäfen stehen. Zweck dieser Symbole ist die Schaffung einer gemeinsamen, universell verständlichen Sprache.
Symbole für geometrische Eigenschaften
- Geradheit — bezeichnet den Zustand, in dem sich alle Punkte auf einer geraden Linie befinden. Die Toleranz wird durch eine von zwei parallelen Linien gebildete Zone festgelegt.
- Ebenheit — bezeichnet den Zustand, in dem sich alle Punkte auf einer Oberfläche in einer Ebene befinden. Die Toleranz wird durch eine von zwei parallelen Ebenen gebildete Zone festgelegt.
- Rundheit— bezeichnet den Zustand, bei dem alle Punkte auf einer Oberfläche kreisförmig angeordnet sind. Die Toleranz wird durch eine von zwei konzentrischen Kreisen begrenzte Zone festgelegt.
- Zylindrizität — bezeichnet den Zustand einer Oberfläche eines Drehkörpers, bei dem alle Punkte den gleichen Abstand zu einer gemeinsamen Achse aufweisen. Die Toleranz wird durch eine von zwei konzentrischen Zylindern begrenzte Zone, innerhalb welcher die Oberfläche liegen muss, festgelegt.
- Profil — Methode zur Tolerierung der Begrenzung von unregelmäßigen Oberflächen, Linien, Bögen oder Normalebenen. Profile können auf einzelne Linienelemente oder die gesamte Oberfläche eines Werkstücks angewendet werden. Die Profiltoleranz wird durch eine gleiche Umgrenzung entlang des theoretisch genauen Profils, innerhalb dessen die Elemente der Oberfläche liegen müssen, festgelegt.
- Neigung — bezeichnet den Zustand einer Oberfläche oder Achse, die in einem angegebenen Winkel (nicht 90°) zu einer Bezugsebene oder -achse steht. Die Toleranzzone wird durch zwei parallele Ebenen, die den angegebenen Winkel zu einer Bezugsebene oder -achse aufweisen, festgelegt.
- Rechtwinkligkeit — bezeichnet den Zustand einer Oberfläche oder Achse, die in einem rechten Winkel zu einer Bezugsebene oder -achse steht. Die Toleranzzone wird folgendermaßen festgelegt: entweder durch eine Zone, die durch zwei Ebenen definiert wird, die rechtwinklig zu einer Bezugsebene oder -achse stehen, oder durch eine Zone, die durch zwei parallele Ebenen definiert wird, die rechtwinklig zur Bezugsachse stehen.
- Parallelität — bezeichnet den Zustand einer Oberfläche oder Achse, bei der alle Punkte den gleichen Abstand zu einer Bezugsebene oder -achse aufweisen. Die Toleranzzone wird folgendermaßen festgelegt: entweder durch eine Zone, die durch zwei Ebenen oder Linien definiert wird, die parallel zu einer Bezugsebene oder -achse stehen, oder durch eine zylindrische Toleranzzone, deren Achse parallel zu einer Bezugsachse steht.
- Konzentrizität — bezeichnet den Zustand, bei dem die Achsen aller gegenüberliegenden Elemente einer Oberfläche eines Drehkörpers mit der Achse des Bezugselements übereinstimmen. Die Toleranzzone wird als Zylinder festgelegt, dessen Achse der Bezugsachse entspricht.
- Position — eine Positionstoleranz definiert eine Zone, in der die Mittelachse oder -ebene von der (theoretisch genauen) Position abweichen darf. Theoretisch genaue Maße legen die theoretisch genaue Position von Bezugselementen sowie von zusammenhängenden Geometrieelementen fest. Eine Positionstoleranz ist die gesamte zulässige Positionsabweichung eines Geometrieelements in Bezug auf seinen genauen Ort. Für zylindrische Elemente wie Bohrungen und Außendurchmesser ist die Positionstoleranz in der Regel der Durchmesser der Toleranzzone, in der die Achse des Elements liegen muss. Für Elemente, die nicht rund sind, wie Schlitze und Streifen, ist die Positionstoleranz die Gesamtbreite der Toleranzzone, in der die Mittelebene des Elements liegen muss.
- Rundlauf — begrenzt die kreisförmigen Elemente einer Oberfläche. Die Toleranz findet unabhängige Anwendung auf jede kreisförmige Messposition, wenn das Werkstück um 360° gedreht wird. Wird ein Lauf auf Oberflächen angewendet, die um eine Bezugsachse konstruiert sind, kann er zur Begrenzung der kumulativen Schwankungen von Rundheit und Koaxialität verwendet werden. Wird er auf Oberflächen angewendet, die rechtwinklig zur Bezugsachse konstruiert sind, erfolgt eine Begrenzung der kreisförmigen Elemente einer Ebene.
- Summenlauf — sieht eine Begrenzung aller Oberflächenelemente vor. Die Toleranz findet gleichzeitig auf alle Messpositionen für Kreis und Profil Anwendung, wenn das Werkstück um 360° gedreht wird. Wird ein Summenlauf auf Oberflächen angewendet, die um eine Bezugsachse konstruiert sind, kann er zur Begrenzung der kumulativen Schwankungen von Rundheit, Zylinderform, Geradheit, Koaxialität, Neigung, Konizität und Profil verwendet werden. Wird er auf Oberflächen angewendet, die rechtwinklig zur Bezugsachse konstruiert sind, erfolgt eine Begrenzung der kumulativen Schwankungen von Rechtwinkligkeit und Ebenheit.
