Ottimizzazione di manovre per un manipolatore robotico in ambiente spaziale
Università di Roma La Sapienza
Come disciplina scientifica, la robotica si occupa principalmente dell’analisi del comportamento cinematico e dinamico dei robot manipolatori e del controllo del loro movimento. Un robot manipolatore è in genere costituito da una catena di corpi rigidi connessi tra di loro da giunti, ognuno dei quali fornisce un grado di libertà di movimento relativo, o di tipo rotatorio o di tipo traslatorio. Tutte le attività svolgibili da un manipolatore robotico sono rese molto difficili dall’ambiente spaziale che lo circonda. Infatti il dispiegamento o l’apertura di un qualsiasi sistema automatizzato provoca variazioni nell’assetto dello spacecraft in cui è alloggiato con possibili conseguenze dannose ai fini della missione. Inoltre tutte le manovre effettuate dal manipolatore non devono essere troppo dispendiose in termini energetici in quanto la potenza fornita è limitata. È dunque necessario che le manovre del manipolatore siano “ottime”, nell’ottica di minimizzare i disturbi sulla base e il consumo elettrico per la movimentazione.

Figura 1
L’ottimizzazione delle manovre permette di determinare quei parametri che minimizzano una determinata funzione di costo che può essere rappresentata dalla somma delle coppie di controllo che agiscono sui link o dalle variazioni degli angoli d’assetto dello spacecraft.
Due differenti algoritmi, implementati all’interno di Adams, sono stati utilizzati per ottimizzare le manovre del manipolatore robotico e sono:
- Il GRG Generalized reduced gradient method
- Il SQP Sequential Quadratic Programming
Lo spacecraft progettato (Figura 1) ha caratteristiche comuni con diversi modelli di veicoli spaziali come l' IXV-Intermediate Experimental Vehicle dell'Agenzia Spaziale Europea e il Pride-ISV del CIRA. All’interno di questo modello è stato alloggiato un manipolatore spaziale (Figura 2) ottenuto dimensionando il braccio robotico utilizzato nel programma DEOS (Deutsche Orbital Servicing Mission).

Figura 2
Per poter riprodurre all’interno di Adams l’ambiente spaziale è stata utilizzata una Macro, un file di testo scritto nel linguaggio di programmazione del software, grazie al quale è stato possibile modellare sia la dinamica relativa orbitale tra il target (corpo da afferrare) e la navetta Pride, sia le perturbazioni dovute all’attrazione gravitazionale terrestre. La Macro è uno strumento molto efficace in quanto permette di applicare forze e coppie per n corpi attraverso un unico comando nel Command navigator di Adams.
L'ambiente spaziale perciò è stato modellato attraverso le coppie gravitazionali e le equazioni di Hill, quest’ultime descrivono la dinamica relativa dei corpi orbitanti. In particolare per il nostro studio è stata riprodotta la configurazione con orbita relativa ellittica potendo studiare due diverse punti di approccio, R-bar e il V-bar (Figura 3).
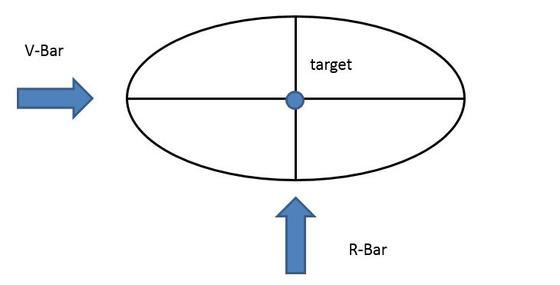

Figura 3
Le manovre compiute che verranno ottimizzate sono il dispiegamento e il grasping:
-Nella prima vengono assegnati gli angoli di dispiegamento in modo tale che in sistema di controllo porti il manipolatore nella configurazione desiderata (Figura4). Le variabili da ottimizzare sono i guadagni del sistema di controllo.


Figura 4
-La seconda consiste nel portare l’end-effector, ovvero la “mano” del manipolatore, a ridosso del target in modo tale da permettere alle pinze di afferrare il corpo desiderato (Figura 5). Le variabili ottimizzate oltre che i guadagni del sistema di controllo sono anche gli angoli desiderati tra i diversi link. Nella Figura 5, in cui è ripotata la manovra di grasping in R-bar, lo spacecraft posizionato in V-bar compie ¼ di orbita ellittica (Figura 6) per poi effettuare il dispiegamento del braccio in R-bar. Si può vedere come l’end-effector viene posizionato dal sistema di controllo nella zona verde, che rappresenta la posizione finale che deve raggiungere, al fine di poter afferrare il target rispettando così i vincoli imposti per l'ottimizzazione.
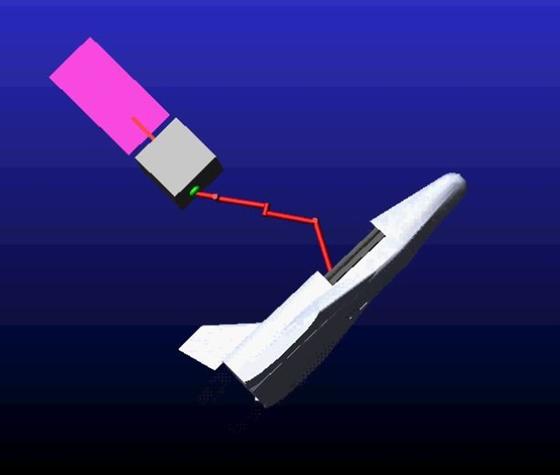
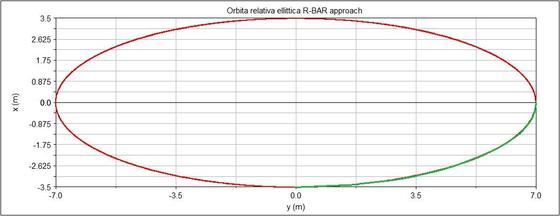

Figura 5
Possibili sviluppi futuri:
- modellazione giunto elastico
- modellazione del link flessibile
- studio dell’interazione delle coppie di controllo sulla flessibilità

Figura 6
Autore:
Andrea De Cesaris
Laurea Magistrale in Ingegneria Spaziale
presso la “Sapienza” Università di Roma