Lo Structural health monitoring (SHM), `e una tecnologia multidisciplinare che fornisce informazioni in tempo reale sullo stato di una struttura e dei suoi singoli componenti attraverso l’utilizzo di un sistema di sensing interno alla struttura stessa. E’ possibile utilizzare le misure di deformazione ottenute dai sensori per ricostruire il campo di spostamento in ogni punto della struttura (shape sensing) e dello stress (stress sensing).
Il Metodo degli elementi finiti inverso (I-FEM o iFEM ) consente di sviluppare algoritmi per lo shape sensing che siano efficienti e applicabili a varie topologie strutturali e condizioni al contorno. Esso presenta analogie con il metodo degli elementi finiti nella suddivisione della struttura in elementi e nella descrizione degli spostamenti dell’elemento in funzione degli spostamenti nodali mediante le funzioni di forma. Il sistema di equazioni lineari che descrive il problema, e quindi le matrici di rigidezza e il vettore dei carichi nodali equivalenti degli elementi finiti inversi, viene ottenuto a seguito della minimizzazione di un opportuno funzionale di errore ai minimi quadrati, con il quale si impone che le deformazioni della soluzione coincidano con le deformazioni misurate dai sensori nei punti in cui sono posizionati.
Lo scopo del presente elaborato è descrivere l’implementazione di un elemento finito inverso quadrilatero a quattro nodi in Marc attraverso l’utilizzo delle user subroutines in modo da poter utilizzare appieno le potenzialit`a del solutore e utilizzare il pre e il post-processore di Mentat.
L’elemento finito inverso implementato verrà quindi utilizzato per una validazione del metodo agli elementi finiti inverso per la ricostruzione del campo di spostamento, delle deformazioni e degli stress di strutture a guscio di geometria complessa tridimensionale, tra cui una semiala di un aliante. Nell’ambito di questo lavoro le misure delle deformazioni, che costituiscono l’input del problema inverso non sono misurate effettivamente da sensori, bensì sono fittizie e sono calcolate attraverso il metodo degli elementi finiti diretto.
Le quattro user subroutines utilizzate per implementare la formulazione dell’elemento finito inverso sono:
- ubginc: chiamata all’inizio dell’incremento 0 e utilizzata per leggere i file di input e salvarne i dati in delle variabili globali che verranno utilizzate dalle altre subroutines
- ufconn: utilizzata per modificare l’element type di un elemento. Bisognerà infatti assegnare agli elementi finiti inversi l’element type -75
- uselem: utilizzata per definire la matrice di rigidezza dell’elemento e, a partire dagli spostamenti, calcolare i vettori contenenti le deformazioni e gli sforzi generalizzati
- forcdt: utilizzata per assegnare il vettore dei carichi nodali ad ogni nodo degli elementi finiti inversi
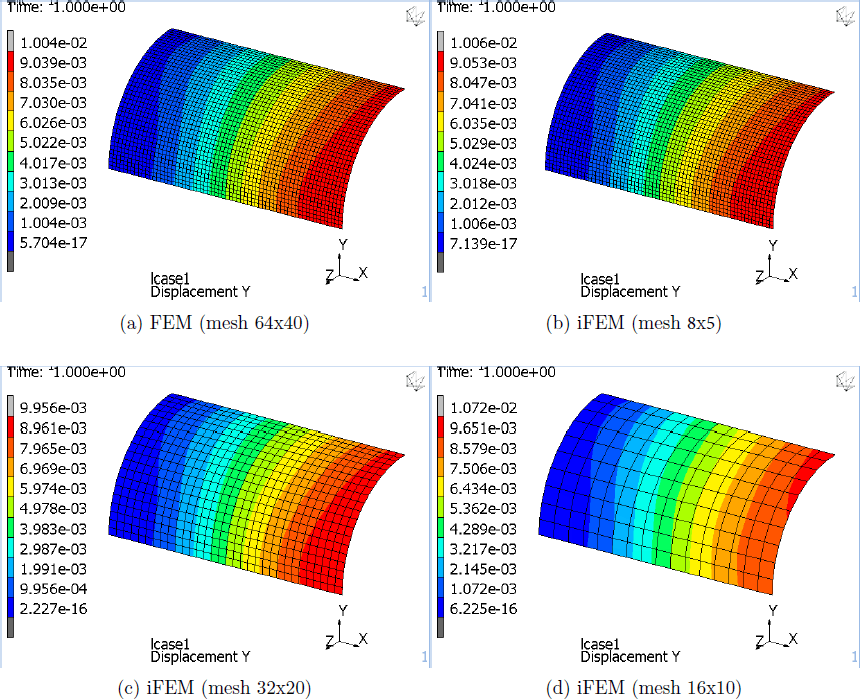
Uno dei casi studio considerati è quello di un guscio a forma di quarto di cilindro incastrato ad una estremità al quale `e stato applicato, sull’altra estremità, un campo di spostamenti parallelo all’asse y globale. Dopo aver calcolato la soluzione con il metodo degli elementi finiti diretto per una mesh formata da 2560 elementi si sono utilizzate le deformazioni in corrispondenza dei centri geometrici degli elementi del modello agli elementi finiti inverso. Nella Figura 1 vengono riportati i model plot degli spostamenti del guscio al variare della mesh.
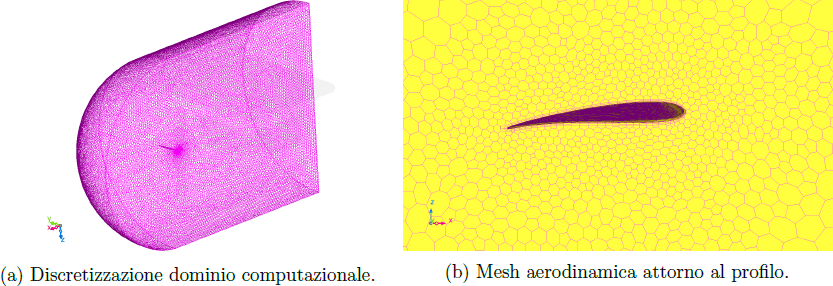
In seguito si è effettuato lo studio di un’applicazione in campo aeronautico, in particolare una semiala di un aliante. Per calcolare la distribuzione della pressione che agisce sulla semiala si effettua un’analisi CFD con il software MSC Cradle per la condizione di crociera dell’aliante, utilizzando 407612 elementi poliedrici per la mesh aerodinamica (Figura 2). Tramite il tool scConverter è possibile inserire i carichi di pressione calcolati con MSC Cradle all’interno del modello strutturale della semiala.
E’ quindi possibile, dopo aver calcolato la soluzione col metodo degli elementi finiti diretto, utilizzare i valori delle deformazioni in corrispondenza dei centri geometrici degli elementi finiti inversi per ricostruire la soluzione con il metodo degli elementi finiti inverso. Nella Figura 3 vengono confrontate le deformate calcolate con il metodo degli elementi finiti diretto e inverso, utilizzando mesh rispettivamente di 20209 e 5873 elementi.

Nelle Figure 4, 5, 6 vengono riportati gli sforzi sul dorso della semiala della soluzione FEM e della soluzione iFEM, modificando i range dei plot in modo da farli coincidere.
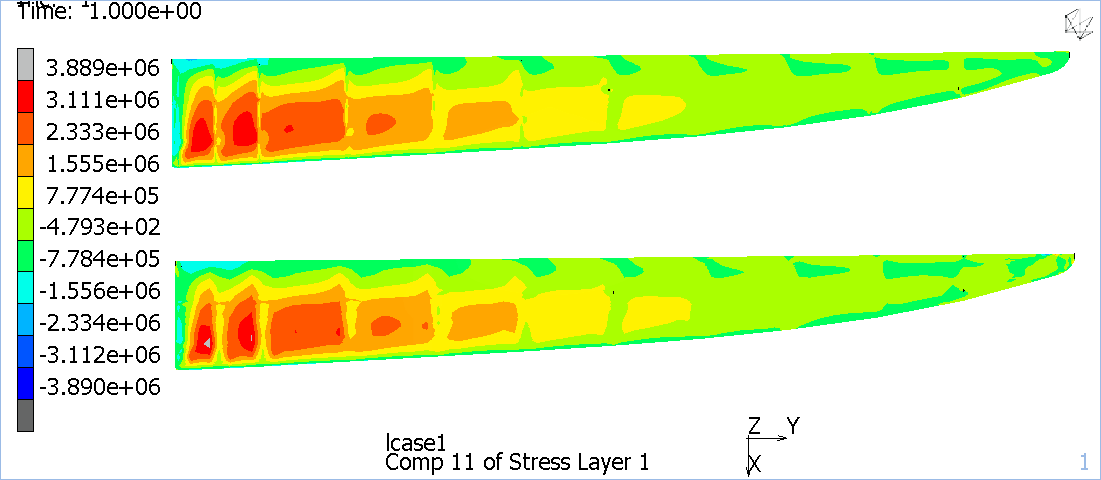
Figura 4: Sforzo σ11 sul dorso (in alto soluzione FEM in basso soluzione iFEM).
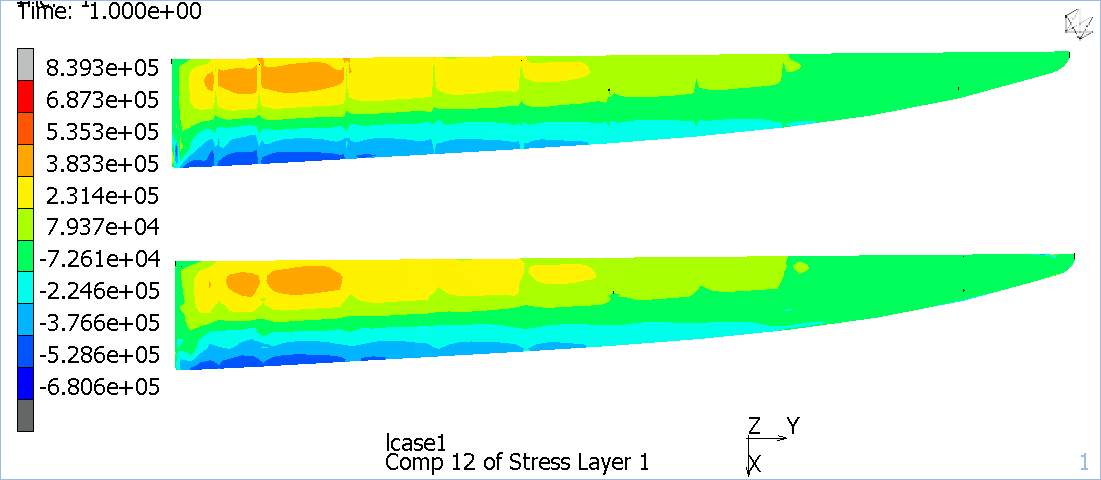
Figura 5: Sforzo σ22 sul dorso (in alto soluzione FEM in basso soluzione iFEM).
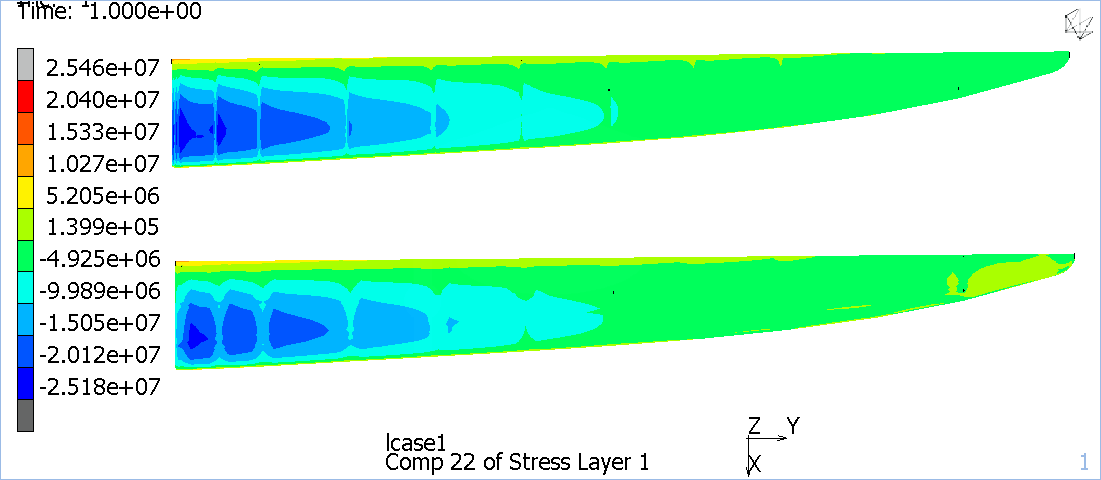
E’ stata effettuata inoltre un’analisi sull’accuratezza del metodo al variare del numero di sensori per una determinata mesh, utilizzando i cosiddetti elementi strain-less, ovvero elementi nei cui centri geometrici non è disponibile una misura della deformazione.
Marco Davini
Relatori: Luca Lampani, Fabio Scannavino (Hexagon)
Università La Sapienza di Roma. Anno Accademico 2021/2022