Feasibility study of rubber mounted pillar for pleasure yacht and passenger yacht

INTRODUZIONE

A bordo delle navi ci sono diverse fonti di vibrazione eccitanti, di solito situate all’estremità di poppa della nave e nella parte inferiore dello scafo. La ricerca di creare navi sempre più veloci ed economicamente sostenibili si discosta dalla ricerca di ambienti sempre più silenziosi che soddisfino le nostre aspettative. Bisogna quindi iniziare a sviluppare nuove soluzioni, nuove tecnologie, al fine di assottigliare la grossa discrepanza tra le due richieste.

Qualsiasi attività in cui siano presenti macchine con masse in movimento producono vibrazioni, urti e rumori che sono da considerare fattori inquinanti per la vita dell’uomo. Le vibrazioni di una nave posso essere di vario tipo come quelle proprie dello scafo, prodotte dalle eliche, dai motori, dai gruppi elettrogeni e quindi da tutti gli impianti che hanno motori con masse rotanti o alternative. Essi generano vibrazioni stazionarie che generano un carico ciclico continuo sulle strutture e un disturbo sulle persone quando il fenomeno è percepito come vibrazione del ponte o rumore. La sala macchine è la zona con il maggior numero di sorgenti e per questo lo sviluppo della tesi sarà improntato sullo studio dei puntelli in quanto sono collegamenti rigidi tra i due ponti.

In questa tesi, lo studio del funzionamento di gomme montata su puntelli è stato fatto usando l’analisi numerica, mediate MSC Natran e Patran,  con lo scopo di determinare, in una prima analisi, se possono essere usati per yacht e quale sia il loro impatto in termini di comportamento strutturale dell’intera barca e in termini di propagazione delle vibrazioni. Un moke up di una struttura semplificata di uno yacht è stata numericamente riprodotta per rappresentare nella maniera più semplice uno scenario reale ma permettendo di controllare tutti i parametri in gioco.

Il primo step è naturalmente verificare il funzionamento del puntello applicando una pressione sull’upper deck per simulare una reale condizione di operabilità, con le appropriate condizioni al contorno.

Fare una analisi numerica della gomma è molto difficile e lungo ma analizzando il comportamento di essa è possibile approssimare la gomma come una molla lineare 1D. Questa approssimazione è molto alta perchè in realtà è un materiale non lineare.

Il secondo step è l’analisi modale. Questa analisi è molto importante perché dice quali frequenze sono dannose così da poter trovare quali sono le condizioni o le frequenze eccitatorie presenti a bordo che possono portare alla risonanza o al collasso della struttura.

Ma per vedere la reale influenza di tutte le frequenze sulla struttura è necessario usare l’analisi di risposta in frequenza la quale restituisce la reale risposta della struttura sottoposta a un carico eccitatorio in termini di spostamento, velocità e accelerazione.

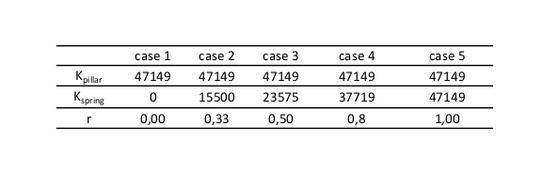
Per distinguere le differenti costanti elastiche usate in ogni test è introdotto un nuovo coefficiente ,r, che è il rapporto tra il modulo elastico del puntello K_pillar  e il modulo di elasticità della molla usata nel test K_spring.

r=0 è il caso dove non c’è l’elemento molla e puntello, mentre r=1 indica il caso con puntello standard senza molla

ANALISI STATICA

Il primo step dell’analisi preliminare della gomma montata su puntelli è di verificare se essi mantengono il ruolo strutturale che gli spetta. In particolare è stato scoperto che non ci sono significanti svantaggi nell’usare la gomma come isolante nei puntelli, e dal comportamento globale appare essere il solito del puntello standard. Al fine di verificare l’approssimazione eseguita è stato creato un modello con gomma 3D da comparare con il modello di gomma monodimensionale rappresentata da una molla. Dal risultato si è visto che per materiale lineare l’approssimazione corretta.

NORMAL MODES

In questo step è possibile trovare attraverso la frequenza naturale e la mode shape della struttura senza carico applicato ed è molto importante valutare l’interazione dinamica per esempio, tra una macchina rotante e la sua struttura di supporto. è necessario trovare la frequenza operativa della macchina e deve essere lontana dalla frequenza naturale della struttura (che si trova attraverso l’analisi modale) per evitare una condizione di risonanza che può portare al danneggiamento della struttura.

L’equazione alla base di questa analisi dipende anche dalle forze elastiche e inerziali, infatti cambiando la rigidezza del sistema cambia il risultato.

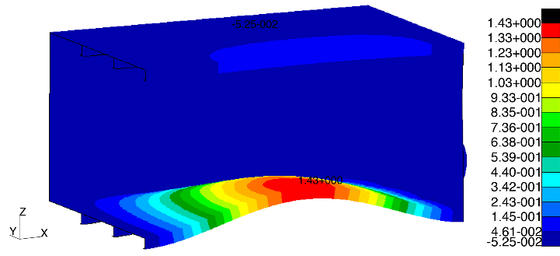
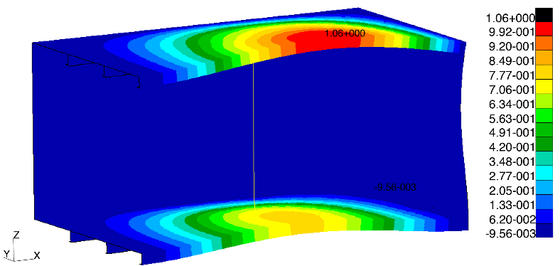
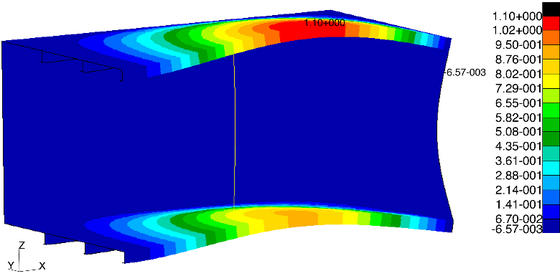
Per esempio una mode shape a 18 Hz per la condizione senza puntello (IMMAGINE 3) può essere trovata per la condizione con puntello alla frequenza di 16 Hz (IMMAGINE 4) dove anche l’upper deck va in risonanza. In questo caso l’incremento di rigidezza a causa del puntello dovrebbe corrispondere un incremento della frequenza naturale, ma in questo caso l’aggiunta del puntello deve essere vista come una connessione rigida tra i due ponti così che lo spostamento del lower deck è trasmesso all’upper deck che con la sua inerzia si comporta come un elemento smorzante.

Quando la gomma è montata sul puntello la frequenza naturale diventa 15 Hz (IMMAGINE 5) questo perché le strutture sono simili ma la gomma riduce la rigidezza del sistema che riduce la sua frequenza naturale.

RISPOSTA IN FREQUENZA

L’analisi di risposta in frequenza è uno step molto importante, dopo l’analisi modale perchè permette di conoscere la reale risposta della struttura a una singola frequenza in termini di spostamento, velocità e accelerazione.

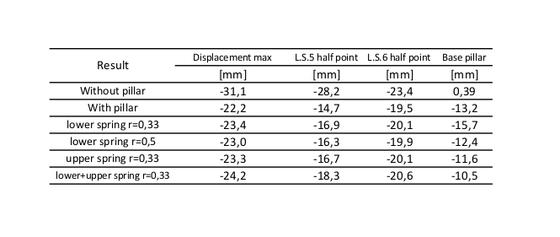
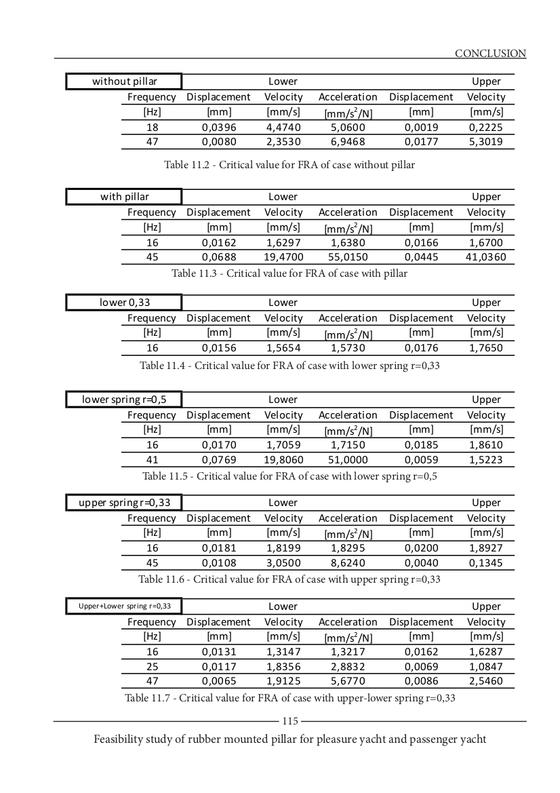
Estrapolando le frequenze critiche(picchi) per ogni caso senza smorzamento scrivendo i corrispondenti valori di spostamento, velocità e accelerazione è possibile creare le seguenti tabelle:

Il caso avente r=0.5 con gomma posta sotto deve essere trattato con particolare attenzione poiché si può apprezzare un picco di risonanza sia in termini di velocità che accelerazione, a 41 Hz. Questo perché in questo caso, il puntello perde la sua funzione di trasferire vibrazioni tra i due ponti e l’assenza di smorzamento crea un grande picco nella funzione di trasferimento in frequenza del lower deck.

Quindi, la progettazione della gomma montata su puntelli deve essere fatta evitando effetti indesiderati di risonanza tra puntello e ponti, modificando la corretta elasticità della gomma stessa.

Questo significa che non è possibile trovare un valore standard dell’elasticità della gomma per garantire l’isolamento dalle vibrazioni ma dipende da una complessa funzione fatta da posizione della gomma, carico agente, vibrazione operativa, condizione operativa di lavoro e molte altre variabili.

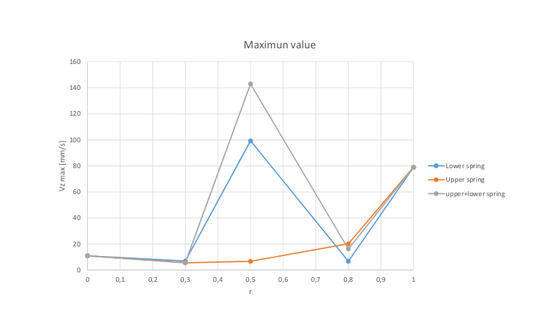
Estrapolando per ogni caso I massimi valori della velocità verticale massima, naturalmente i nodi saranno diversi per ogni caso, è possibile tracciare il grafico in FIGURA dove sull’asse X è rappresentato il coefficiente r. Per r=0 è riportata la situazione senza puntello e molla, mentre per r=1 è riportata la condizione con puntello standard ma senza molla.

Un possibile risultato dovrebbe essere vedere un andamento di incremento dove le curve iniziano da un piccolo valore fino a un valore massimo dato dal puntello standard (r=1) ma il risultato restituisce una risposta contrastante.

Infatti è possibile vedere un picco della curva attorno al valore di r=0.5 per il puntello con gomma inferiore e con molla sopra-sotto. Questa condizione mostra una possibile risonanza per questa rigidezza della molla ma solo con molla sotto e sotto-sopra dove l’inerzia del puntello agisce sull’upper deck ed è isolato dal lower deck.

Una possibile spiegazione di questo fenomeno è data dalla posizione della molla e dall’assenza di smorzamento. Infatti posizionando la molla sopra il puntello collabora con il lower deck in termini di rigidezza ed è più difficile per lui oscillare. Se la molla è posta nella posizione inferiore, quindi con puntello isolato dal lower deck, esso coopera con l’upper deck e la vibrazione generata dalla forza eccitatoria arriva al puntello che è simile a una trave a mensola e in assenza di smorzamento l’energia che arriva dal fianco, dal ponte fino al puntello genera una vibrazione, o meglio, un’oscillazione simile all’effetto di sbandieramento.

Nella posizione sotto-sopra è la condizione peggiore perchè è libero di vibrare in ogni direzione. Naturalmente questi effetti vengono annullati con la presenza dello smorzamento strutturale.

Luca Falcinelli
Università di Genova
Polo G. Marconi – La Spezia

Relatori:

Prof. Ing. Dario Boote
Ing. Gianmarco Vergassola