Modellazione dinamica di un robot a cavi parallelo per applicazioni riabilitative
L’obiettivo di questo progetto è la costruzione di un modello dinamico di un robot a cavi per applicazioni riabilitative (chiamato Stand Trainer) sviluppato dalla Columbia University che ne simuli il comportamento e tramite il quale si possa ricavare lo sforzo esercitato dal paziente durante l’esercizio riabilitativo. Per la simulazione di questo meccanismo, sono stati costruiti tre modelli attuati in modo diverso. Tra questi, si è scelto quello che meglio approssimava il comportamento del sistema reale. Su questo sono poi state applicate le equazioni della dinamica utilizzando i dati raccolti dalla simulazione per raggiungere l’obiettivo sopra descritto.
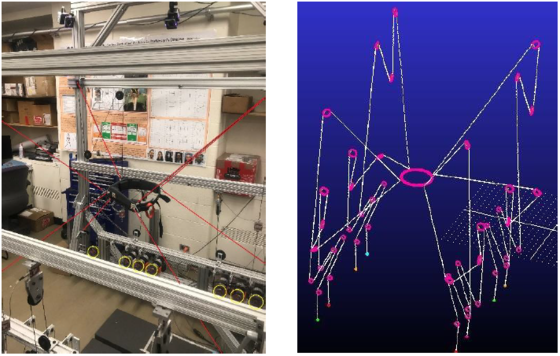
Fig. 1: Confronto tra sistema reale e modello Adams
DESCRIZIONE DEI MODELLI COSTRUITI E DIFFERENZE RISCONTRATE
Prima della costruzione dei modelli, è bene precisare che è stato necessario effettuare un test su un soggetto sano, a cui sono state applicate delle forzanti dai cavi del robot (precedentemente definite). In questo modo, varie grandezze sono state misurate e registrate: le tensioni applicate ai cavi, le velocità dei motori a cui i cavi stessi sono avvolti e il moto cartesiano del centro di massa della persona. In questo modo, si avevano a disposizione gli elementi necessari da utilizzare come input nelle simulazioni e verificare che il comportamento fosse in linea con quello del sistema reale.
I modelli costruiti nell’ambiente Adams prevedono alcune semplificazioni rispetto al sistema “robot-paziente”:
- la massa della cintura è pari a quella del soggetto con cui sono stati effettuati i test (90 kg) e la sua matrice d’inerzia calcolata rispetto al sistema baricentrico possiede solo termini diagonali che assumono un valore pari a quelli medi di una persona adulta;
- i cavi sono privi di massa;
- il sistema risulta simmetrico rispetto al piano sagittale;
- la cintura assume una forma toroidale del diametro medio del bacino di una persona adulta ed è modellata come un corpo rigido (non ci sono né azioni elastiche, né viscose).
I tre modelli costruiti hanno caratteristiche diverse in termini di attuazione, ovvero sono diversi i gradi di libertà attuati e le forze applicate.
In particolare, queste sono le loro caratteristiche:
- Modello 1: vengono applicate le velocità dei motori tramite variabili di stato, in cui, in base alla rotazione di un elemento “biella” a cui si attacca la parte terminale del cavo, quest’ultimo varia la sua lunghezza e muove così la cintura.
- Modello 2: vengono applicate le tensioni ai cavi. In questo caso non si hanno più gli elementi “biella” come in precedenza, ma aggiungendo una puleggia in più in modo da mantenere verticale il cavo, sono state introdotte delle sfere di massa trascurabile a cui è stata attaccata l’estremità del cavo. In questo modo, la tensione al cavo è applicata applicando una forza verso il basso in direzione verticale alla sfera, la quale viene vincolata a scorrere solamente in quella direzione. In questo modello, non essendo imposto il moto alla cintura, è necessario implementare un ulteriore cavo che permetta al sistema di non cadere a causa della gravità, in quanto le forze esplicate dai cavi non permettono di sollevare completamente il paziente durante l’esercizio riabilitativo.
- Modello 3: vengono imposte le tensioni ai cavi come nel modello precedente, ma in questo caso sono anche imposti i moti nelle tre direzioni al centro di massa della cintura.
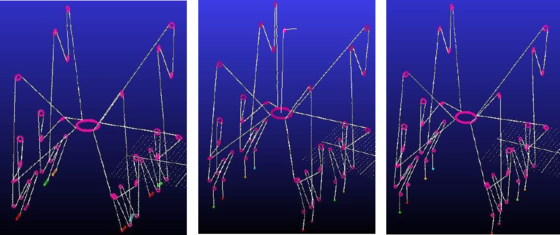
Fig. 2: Modelli costruiti per simulare il comportamento del robot a cavi oggetto dello studio.
Per quanto riguarda il comportamento di questi tre modelli appena introdotti, risulta essere molto diverso l’uno dall’altro.
In primo luogo, il Modello 1 presenta un moto del centro di massa della cintura in linea con quello registrato nei test sul campo, ma le forze applicate dai cavi sono di svariati ordini di grandezza più elevate rispetto a quelle effettivamente applicate. Questo poiché si sta utilizzando un controllo di posizione del robot che va a inficiare sul suo comportamento dinamico, applicando forze troppo elevate sul paziente che a quel punto sarebbe soggetto ad un infortunio.
Secondariamente, l’applicazione del Modello 2 presenta anch’essa alcune problematiche. Infatti, nonostante le tensioni agenti sui cavi e di conseguenza le forze applicate sul paziente, siano in linea coi risultati reali, il moto del centro di massa della cintura risulta completamente diverso da quello registrato, in quanto il paziente non reagisce alle forze che gli vengono applicate, per cui il moto risulta molto rallentato rispetto a quello che in realtà accade.
L’ultimo modello presentato (Modello 3) risulta invece essere quello che possiede un comportamento più in linea rispetto a quello reale: sia il moto della cintura che le forze che i cavi esercitano sul paziente risultano essere esattamente uguali a quelli registrati (poiché questi ultimi sono stati imposti).
A questo punto, il modello scelto per le analisi dinamiche che porteranno all’obiettivo dello studio è il Modello 3: applicando il moto al centro di massa della cintura e le tensioni ai cavi, si ottiene un modello che simula con buona approssimazione il comportamento del sistema reale.
RISULTATI OTTENUTI
Tramite la simulazione del comportamento del sistema “robot-paziente” reale, è possibile andare a ricavare tutte le forze che agiscono sulla cintura, utilizzando le equazioni della dinamica del sistema.
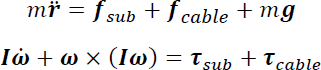
Dove si hanno:
r: vettore posizione del centro di massa della cintura;
m: massa della cintura;
I: matrice d’inerzia della cintura rispetto al sistema baricentrico;
ω: velocità angolare del centro di massa della cintura;
fcable: forza che i cavi esercitano sulla cintura;
fsub: forza che esercita il paziente durante la prova;
τcable: coppia che i cavi esercitano sulla cintura;
τsub: coppia che il paziente esercita durante la prova;
g: accelerazione di gravità.
Tramite l’analisi di post-processing è possibile ricavare quelle che sono le forze e le coppie agenti sui punti di ancoraggio dei cavi sulla cintura. Riportandole tutte al centro di massa del sistema e sommandole si ottengono i termini indicati nelle equazioni precedenti come fcable e τcable.
A questo punto, noto completamente il moto del sistema, note le inerzie e note le forze che agiscono sul paziente, è possibile, tramite una banale equazione algebrica, ricavare lo sforzo del paziente durante l’esercizio riabilitativo. Riformulando le equazioni precedenti si ottiene:
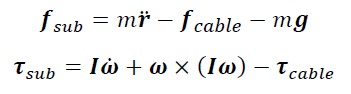
Applicate in ogni istante di tempo, queste equazioni permettono di verificare l’andamento dello sforzo del paziente. Ciò risulta molto importante da un punto di vista riabilitativo, in quanto a seconda di che tipo di disabilità il paziente stesso presenta, è possibile effettuare esercizi mirati per fargli sviluppare una azione che vada ad attivare la muscolatura necessaria. Effettuando più esercizi nel tempo, si potrà altresì valutare il miglioramento delle prestazioni del paziente durante l’esercizio e se effettivamente le forze imposte dai cavi rendano utile o meno l’allenamento.
Una volta ricavati gli sforzi come da equazioni sopra riportate, è necessario filtrare i risultati ottenuti, in quanto come detto in precedenza, l’assenza di elasticità e smorzamento, combinata con il super-vincolamento dato dal meccanismo fa nascere alcuni picchi di forza e coppia ingiustificati, che raggiungono valori molto più elevati di quelli effettivi (pochi ordini di grandezza). È quindi necessario filtrare i dati tramite l’utilizzo di un filtro passa-basso a una frequenza coerente con il tempo di reazione di una persona a fronte dell’azione di una forza esterna (3-4 Hz). Filtrando i risultati a 3 Hz, quello che si ottiene lo si può verificare nei grafici sottostanti.
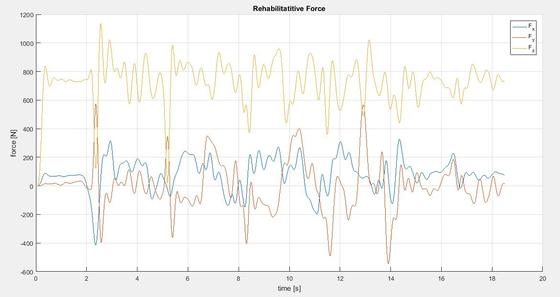
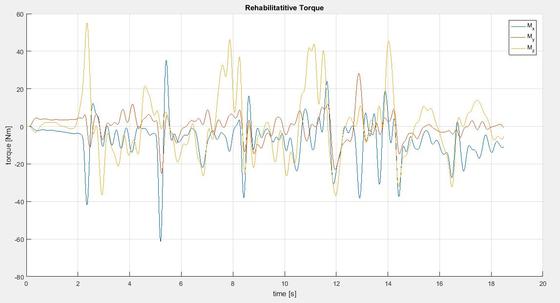
Fig. 3: Forze e coppie riabilitative applicate dal paziente dopo filtraggio dei dati.
Autore:
Enrico Sammarchi
Università di Bologna