Politecnico di Milano
In collaboration with Leonardo Helicopters Division
The work is concerned with the development of a multidisciplinary model of a tiltrotor aircraft actuation system (represented pictorially and schematically in figures 1 and 2), with the scope of adopting it in nonlinear aeroservoelastic analyses. The model integrates the different components and subsystems concerned, namely: the hydraulic servoactuator and its local control loop, the mechanical model of the actuation chain, and the flexibility of the control surface, and includes the description of some fundamental nonlinearities found in the subsystems, among which the most important for aeroelastic purposes is the mechanical freeplay of the control surface, intended as a dead-zone in which no restoring moment is produced by a rotation of the surface.
Figure 1. MSC Adams view of the system
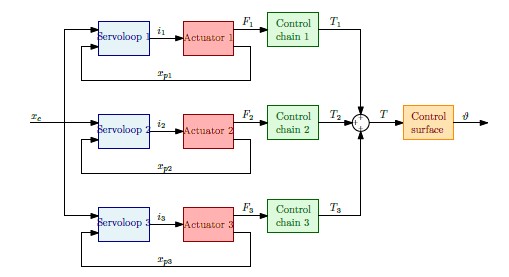
Figure 2. Schematic depiction of the system
The model of the hydraulic actuator is implemented using the Simscape suite contained in Simulink, which allows to construct complex systems starting from simple building blocks that implement differential or algebraic equations describing physical systems. Its control loop, instead, is modelled using Simulink block diagrams. The model is then validated by comparing its response to commanded displacements and external forces with experimental data.
The mechanical model, instead, is implemented using the multibody software MSC Adams. It comprises three identical control chains and also includes the flexibility of both the main and control surfaces in the form of .mnf files extracted from modal analyses performed on FEM models using MSC Nastran.
Figure 3 depicts a simplified drawing of one of the control chains, which is modelled using rigid bodies and ideal joints, except for one joint that is represented by a contact between the two parts that need to interact. The contact has been used in order to include the effect of the gaps which occur between the bolts and bearings present in each joint, and which accumulate creating the overall freeplay effect. The contact geometry has been simplified, as visible in figure 4, and only gaps in the radial direction are accounted for, by constraining the relative lateral motion between the two parts.
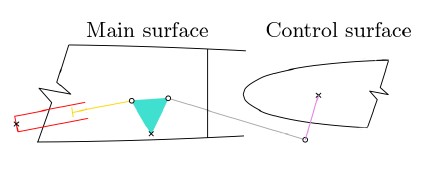
Figure 3. Drawing of the control chain
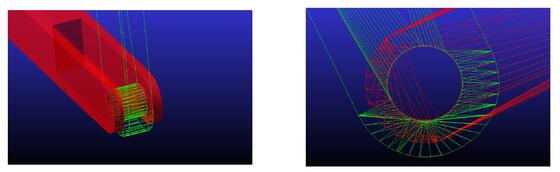
Figure 4. Views of the contact geometry
The main part of the work consists in the cosimulation of the Simscape and Adams models, which is achieved leveraging the cosimulation capabilities of the two software. Figure 5 shows the Adams/Simulink cosimulation model, in which the actuator model has been substituted with linear transfer functions since actuator nonlinear effects are not expected to play an important role in the specific simulations to be run. Indeed, the model is subject to a virtual test aiming to reproduce actual experimental test conditions in which a quasi-static load is applied to the control surface while its rotation is measured. The objective of this test is to reconstruct a rotation – hinge moment curve that should show the freeplay nonlinearity.
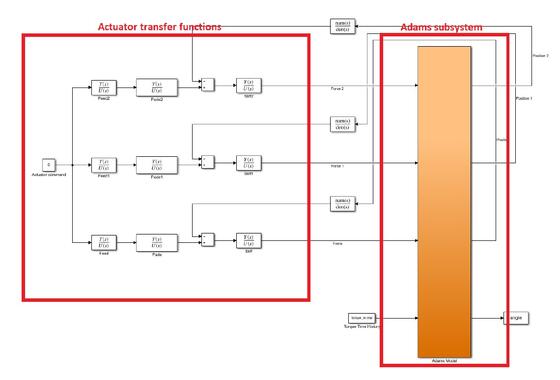
Figure 5. Adams/Simulink model
As figure 6 shows, this behavior is clearly evident both in the experimental data and in the simulated test. However, the peculiar lobes that appear in the experiment are not reproduced by the simulation. This is explained by the fact that this kind of hysteretic phenomenon is linked to friction forces which have not been included in the Adams model of the control chain.

Figure 6. Freeplay test results (Left: simulation, Right: experiment)
The last step of the work consists in a nonlinear aeroservoelastic simulation using a typical section model, which includes this peculiar characteristic of the control surface hinge in lieu of a linear spring in order to show its potential effects, namely a limit cycle oscillation, as visible in figure 7.
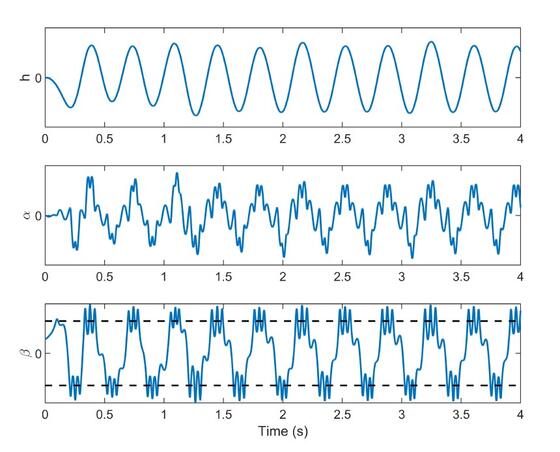
Figure 7. Aeroelastic model LCO (dashed: freeplay amplitude)
MSc Thesis by: Federico Pellegrino
Supervisor: Prof. Giuseppe Quaranta
Company tutor: Ing. Alberto Angelo Trezzini