Dynamic Analysis and Design of a 6-dof Parallel Mechanism Based on 6-PUS Kinematic Chains

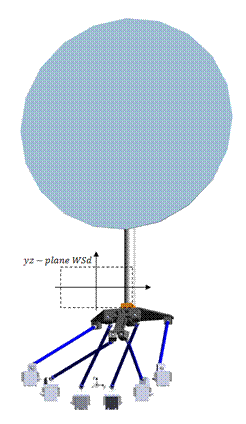
The mechanism under study is a 6-dof fully parallel manipulator with 6 independent kinematic chains of PUS type. Each kinematic chain is consist of an actuated prismatic joint on the base which is followed by an universal joint connecting the constant length link to the sliding body, which itself is followed by a spherical joint on the connection between link and platform.

This robotic platform is going to be applied as a test rig to perform unsteady aerodynamic experiments inside the wind tunnel. It is intended to function as emulator in the loop of the sea to simulate the real working condition of the offshore structures.

Despite advantageous performance features of parallel robots in terms of precise accuracy, fast operation speed, and high load capacities with respect to classic serial manipulators their application have been limited in practice. This is mainly due to their complexity of kinematic and dynamics problem which also lead to difficulty of establishing a control law based on the dynamic model.
 

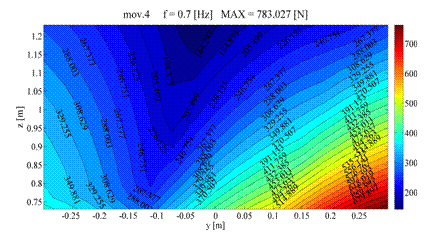
The multibody dynamics software Adams has been applied to perform the simulations and evaluate the dynamics of the mechanism. We aim to realize the dynamics of the robot for its working condition of TCP inside the desired work space. In particular we divide the desired works space of the TCP of the robot in the yz plane into a grid of 17×17 points. For each single coordinate of the TCP of the platform – three translational and three rotational components: X = [x y z α β γ] ^_T - we impose a sinusoidal motion separately, at every point in the grid inside the desired work space. At any point of the working grid all the combination of three set of orientation  {-15°,0°,+15°} for each angle of the local frame of the platform with respect to the fixed reference frame are considered.

It is necessary to perform a huge number of simulations with different motion laws at each point of the desired work space. In particular for a unique set of geometrical parameters of the mechanism, and a specific application with specified frequency and amplitudes of motion we need to perform 16524 numbers of simulations to realize the behavior of mechanism inside its desired work space, which seems impossible to perform manually. The solution is to integrate Macros together with the model in Adams to automatically perform the repetitive procedures.

It is important to notice that the imported model consists of too many bodies that must be connected to each other by introducing proper constraints. This leads to increase the load of data to be executed at each single simulation. To solve the problem of increased execution time, it is possible to avoid saving the default results sets automatically, and then create some requests for the quantities that are more of interest, and then write the data of each request on a file on hard disk for each simulation.

 

The flexibility of the environment created by the integration of Macros with the Adams/View model, allows us to easily apply modifications in the model whenever it would be necessary and study the dynamics of the new mechanism.