Analysis of the influence of design parameters of a vibratory feeder through multibody simulation
Introduction
Vibratory feeders are devices adopted in manufacturing plants to convey products by means of mechanical vibrations of a surface called the tray.The goal of this thesis is to investigate the influence of the principal feeding parameters on the speed of feeding parts over the tray. The objective is dual: first it enables to achieve the optimal feeding condition to increase feeding speed, secondly it enables to neglect those design parameters that are irrelevant during the design-phase of vibratory feeders.
Analysis through Adams and results
The multibody simulator developed in Adams is shown in Figure 1. The simulator is simply composed by a rigid tray where parts flow due to the harmonic motion of the surface. Contact forces are adopted to ensure the motion of the bodies over the tray. It is worth to notice that this kind of system is traditionally excited by means of harmonic forces whose amplitude and phase depends upon the system characteristics, e.g. inertial parameters, stiffness of the supporting springs, flexibility of the tray, length of the tray, distribution of the actuation forces (see Figure 1.a). Further, the system is underactuated, i.e. the number of independent actuators is smaller with respect to the number of degrees of freedom of the system. Hence, it is not trivial to ensure that the excitation forces are optimally in order to ensure that the system behaves as if the tray is rigid, i.e. the displacements of each node of the tray is ensured to be equal to the other and the nodal rotation are negligible. In order to cope with this task excitation forces should be computed through an inverse dynamic approach as the one proposed by the investigators in [1]. Finally, once the feeder is properly controlled, and a rigid-like behavior for the tray is obtained by means of a proper choice of the excitation it is possible to investigate the influence of the design parameters in several feeding conditions exploiting the rigid model provided in Figure 1.b and used in this thesis.
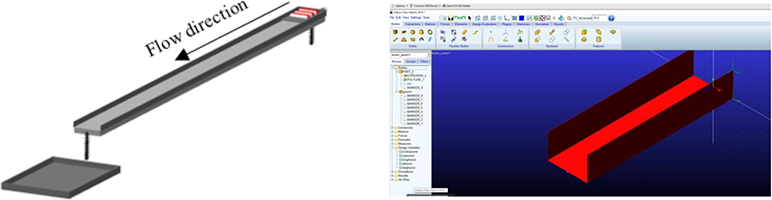
Figure 1. The Adams simulator of the vibratory feeder: flexible feeder (a) and rigid counterpart (b).
Simulations are performed by varying:
- throw angle: the orientation of the actuation forces with respect to the tray;
- mass of the part conveyed;
- excitation frequency;
- amplitude of the tray displacements;
- inclination of the tray;
- static and dynamic friction coefficients;
- shape of the part conveyed (see Figure 2): in particular sphericity index is exploited for a systematic analysis;
- contact forces parameters.
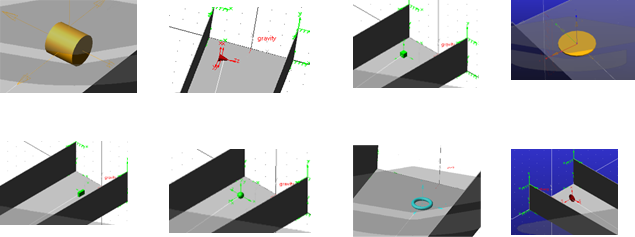
Figure 2. Part conveyed with different shapes in the Adams multibody simulator.
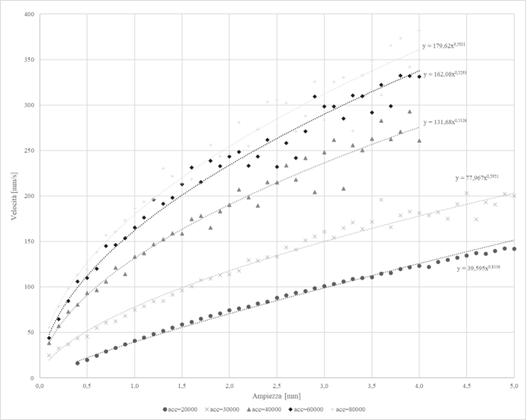
Figure 3. Example of application of the obtained metamodels.
Conclusions
The results achieved through Adams simulations evidences the capability of adopting the simulator to understand the phenomena of parts feeding of vibratory feeders and in particular of determining the parameters of greatest interest. Further, the analysis performed enabled to determine some metamodels that provide some simple and useful relations to predict the feeding speed as a function of several design parameters. The simulator effectiveness has been also corroborated by the great agreement of the simulation results with several experimental and theoretical results proposed in the literature (e.g. [2], [3]).References
[1] Belotti, R., Richiedei, D., Tamellin, I., & Trevisani, A. (2021). Response optimization of underactuated vibration generators through dynamic structural modification and shaping of the excitation forces. The International Journal of Advanced Manufacturing Technology, 112(1), 505-524.[2] Lim, G. H. (1997). On the conveying velocity of a vibratory feeder. Computers & structures, 62(1), 197-203.
[3] Chandravanshi, M. L., & Mukhopadhyay, A. K. (2017). Dynamic analysis of vibratory feeder and their effect on feed particle speed on conveying surface. Measurement, 101, 145-156.
Author: Mattia Cestonaro
Supervisor: Prof. Dario Richiedei, dario.richiedei@unipd.it
Co-supervisor: Ing. Iacopo Tamellin, iacopo.tamellin@unipd.it